NablaVis: un tool didattico e interattivo per visualizzare tre applicazioni del Teorema di Stokes
Questo post introduce NablaVis, un'applicazione web didattica e interattiva progettata per aiutare studenti a visualizzare e comprendere i teoremi fondamentali del calcolo vettoriale attraverso scene 3D interattive. Lo strumento permette agli utenti di esplorare campi scalari e vettoriali, manipolare percorsi e superfici e osservare la verifica numerica in tempo reale delle relazioni matematiche.
NablaVis copre tre applicazioni fondamentali che sono tutte unificate nel quadro generale del Teorema di Stokes:
- Teorema del Gradiente - relazione tra un integrale di linea di un campo gradiente e la differenza dei valori del campo scalare agli estremi
- Teorema del Rotore - relazione tra un integrale di linea lungo una curva chiusa e un integrale di superficie del rotore sulla superficie racchiusa
- Teorema della Divergenza - relazione tra il flusso di un campo vettoriale attraverso una superficie chiusa e la divergenza sul volume racchiuso
L'applicazione è disponibile e accessibile liberamente all'indirizzo: https://computationalmindset.com/apps/NablaVis
Filosofia Educativa
I concetti del calcolo vettoriale come gradiente, rotore e divergenza sono spesso difficili da comprendere per gli studenti attraverso le sole presentazioni tradizionali dei libri di testo. NablaVis colma questa lacuna rendendo questi concetti matematici astratti tangibili e interattivi. Invece di un apprendimento passivo, gli studenti possono manipolare oggetti matematici in tempo reale e osservare immediatamente come i cambiamenti influenzano la verifica dei teoremi.
Lo strumento enfatizza l'esplorazione pratica: gli utenti possono trascinare gli estremi dei percorsi, regolare le superfici, cambiare i campi vettoriali e osservare mentre l'applicazione calcola e confronta istantaneamente entrambi i membri dell'equazione di ciascun teorema. Questo feedback visivo e numerico immediato aiuta a costruire l'intuizione su cosa significano realmente questi teoremi e perché funzionano.
Il Teorema del Gradiente
Il Teorema del Gradiente afferma che per un campo scalare $f$ e un percorso dal punto $P$ al punto $Q$: $$\int_C \nabla f \cdot \mathrm{d}\mathbf{r} = f(Q) - f(P)$$
In NablaVis, questo teorema è visualizzato attraverso:
- Rappresentazione 3D del campo scalare: Una mappa di altezza dove la coordinata z rappresenta il valore del campo scalare $f(x,y)$
- Percorso interattivo: Una curva che collega i punti P e Q che può essere modificata cliccando sul terreno per riposizionare gli estremi
- Verifica in tempo reale: L'HUD mostra sia $f(Q) - f(P)$ che l'integrale di linea calcolato $\int_C \nabla f \cdot \mathrm{d}\mathbf{r}$, confermando che sono uguali indipendentemente dal percorso scelto
Quattro campi scalari predefiniti sono disponibili per l'esplorazione:
- Paraboloide: $f(x,y) = x^2 + y^2$ - una semplice superficie convessa
- Superficie a Sella: $f(x,y) = x^2 - y^2$ - dimostra un paraboloide iperbolico
- Picco Gaussiano: $f(x,y) = e^-(x^2 + y^2)$ - una superficie liscia a forma di campana
- Collina e Valle: Un terreno piú complesso con piú punti critici
La visualizzazione dimostra chiaramente una proprietà chiave dei campi gradiente: sono conservativi, il che significa che l'integrale di linea dipende solo dagli estremi, non dal percorso scelto tra di essi.
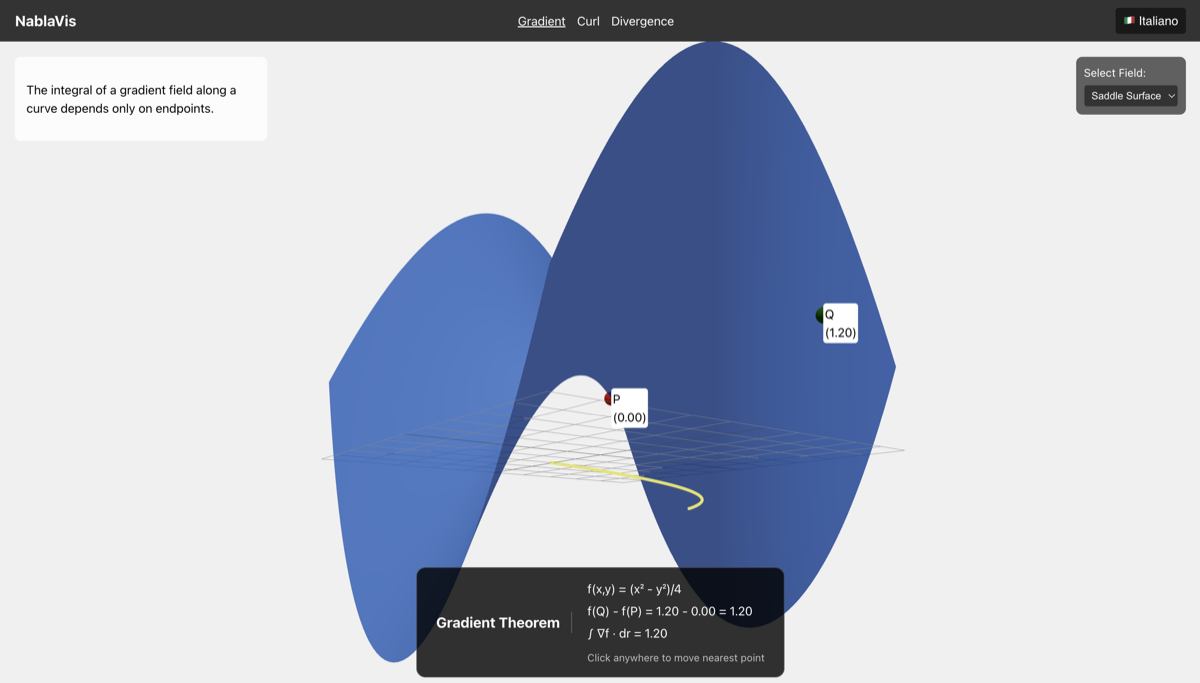
Il percorso collega i punti P e Q, e l'HUD verifica che $\int_C \nabla f \cdot \mathrm{d}\mathbf{r} = f(Q) - f(P)$.
Il Teorema del Rotore
Il Teorema del Rotore mette in relazione la circuitazione di un campo vettoriale lungo una curva chiusa con il flusso del suo rotore attraverso la superficie racchiusa: $$\oint_C \mathbf{F} \cdot \mathrm{d}\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{S}$$
La visualizzazione presenta:
- Campo vettoriale 2D: Frecce sul piano xy che mostrano il campo vettoriale $\mathbf{F}(x,y)$
- Percorso circolare: Una curva chiusa $C$ che delimita una superficie $S$
- Verifica matematica: Confronto in tempo reale della circuitazione $\oint_C \mathbf{F} \cdot \mathrm{d}\mathbf{r}$ (membro sinistro) con l'integrale di superficie $\iint_S (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{S}$ (membro destro)
Quattro campi vettoriali predefiniti illustrano comportamenti diversi:
- Rotazione Semplice: $\mathbf{F} = (-y, x)$ - rotazione uniforme intorno all'origine
- Flusso di Taglio: $\mathbf{F} = (y, 0)$ - movimento di taglio orizzontale
- Spirale Espansiva: Combinazione di rotazione ed espansione radiale
- Campo a Sella: Un campo con distribuzione del rotore piú complessa
Questa visualizzazione aiuta gli studenti a comprendere che il rotore misura la "tendenza rotazionale" di un campo vettoriale, e il Teorema del Rotore mette in relazione la rotazione microscopica (rotore in ogni punto) con la circuitazione macroscopica lungo un contorno.
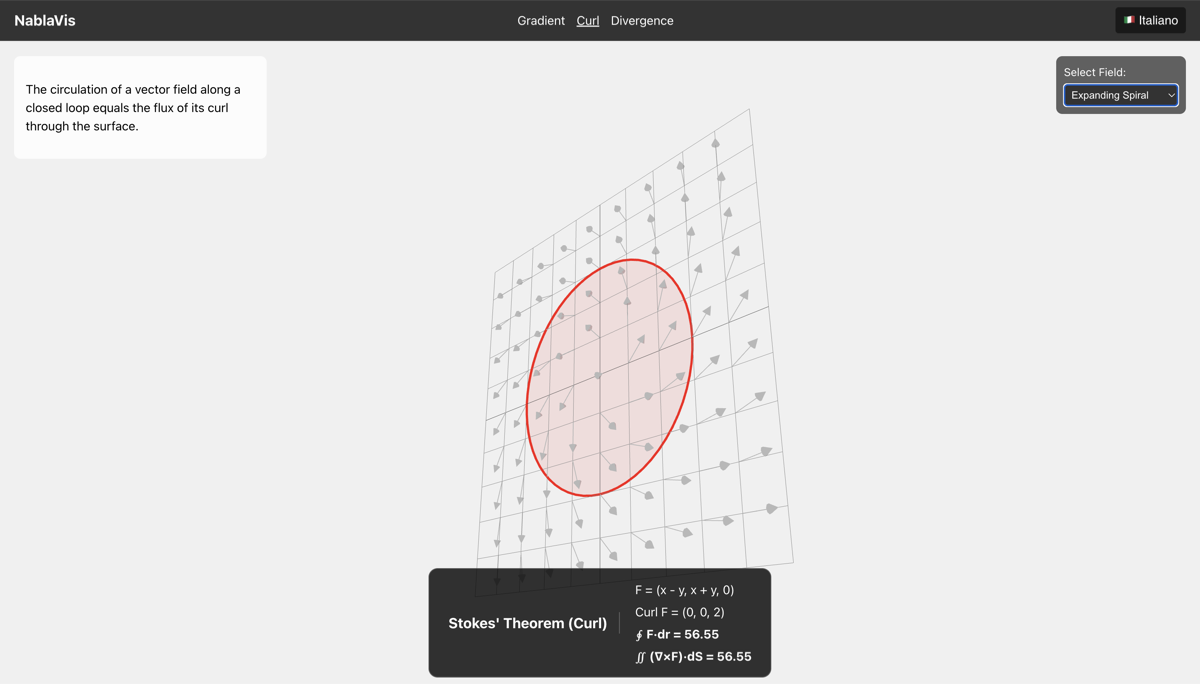
Il percorso circolare delimita una superficie, e l'HUD verifica che $\oint_C \mathbf{F} \cdot \mathrm{d}\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot \mathrm{d}\mathbf{S}$.
Il Teorema della Divergenza
Il Teorema della Divergenza mette in relazione il flusso di un campo vettoriale attraverso una superficie chiusa con la divergenza nel volume racchiuso: $$\iint_S \mathbf{F} \cdot \mathrm{d}\mathbf{S} = \iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V$$
La visualizzazione 3D include:
- Campo vettoriale 3D: Frecce nello spazio tridimensionale che mostrano $\mathbf{F}(x,y,z)$
- Superficie sferica: Una superficie chiusa $S$ che racchiude un volume $V$
- Verifica in tempo reale: Confronto del flusso totale $\iint_S \mathbf{F} \cdot \mathrm{d}\mathbf{S}$ attraverso la superficie con l'integrale di volume $\iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V$
Quattro campi predefiniti dimostrano comportamenti di divergenza diversi:
- Sorgente (Carica Puntiforme): $\mathbf{F} = (x, y, z)$ - flusso radiale verso l'esterno, divergenza positiva
- Pozzo: $\mathbf{F} = (-x, -y, -z)$ - flusso radiale verso l'interno, divergenza negativa
- Campo Uniforme: $\mathbf{F} = (1, 0, 0)$ - campo costante con divergenza zero
- Espansione Verticale: $\mathbf{F} = (0, 0, z)$ - espansione in una sola direzione
La visualizzazione mostra chiaramente che la divergenza misura l'"intensità della sorgente" o l'"intensità del pozzo" in ogni punto - se il campo si sta espandendo verso l'esterno (divergenza positiva) o contraendo verso l'interno (divergenza negativa).

La superficie sferica racchiude un volume, e l'HUD verifica che $\iint_S \mathbf{F} \cdot \mathrm{d}\mathbf{S} = \iiint_V (\nabla \cdot \mathbf{F}) \, \mathrm{d}V$.
Interfaccia Utente e Interazione
NablaVis fornisce un'interfaccia intuitiva con diverse funzionalità chiave:
- HUD in tempo reale (Heads-Up Display): Mostra le formule matematiche, i valori calcolati per entrambi i membri di ciascuna equazione, e la conferma quando il teorema è verificato (i valori coincidono entro una tolleranza numerica)
- Selezioni predefinite: Accesso rapido a campi scalari e vettoriali predefiniti che dimostrano proprietà matematiche interessanti
- Controlli camera 3D: Ruotare, spostare e zoomare per visualizzare le scene da qualsiasi angolazione
- Supporto multilingue: Interfaccia disponibile in inglese e italiano
- Design responsive: Funziona su computer desktop, tablet e dispositivi mobili
- Manipolazione interattiva:
- Per il Teorema del Gradiente: Cliccare sul terreno per spostare gli estremi del percorso
- Per i Teoremi del Rotore e della Divergenza: Osservare come si comportano i diversi campi predefiniti
Implementazione Tecnica
NablaVis è costruito utilizzando tecnologie web moderne che consentono grafica 3D ad alte prestazioni nel browser:
- React 18: Framework UI basato su componenti per costruire la struttura dell'applicazione
- TypeScript: Aggiunge sicurezza dei tipi e migliora la manutenibilità del codice
- Three.js: Libreria grafica 3D standard del settore alimentata da WebGL
- @react-three/fiber: Renderer React per Three.js, che consente la costruzione dichiarativa di scene 3D
- @react-three/drei: Helper e astrazioni utili per pattern 3D comuni
- Vite: Strumento di build moderno che fornisce sviluppo veloce e build di produzione ottimizzate
- React Router (HashRouter): Routing lato client che funziona in qualsiasi ambiente di hosting, comprese le sottocartelle
Gli algoritmi di integrazione numerica calcolano integrali di linea, integrali di superficie e integrali di volume utilizzando metodi di discretizzazione appropriati. Le visualizzazioni di verifica si aggiornano in tempo reale mentre gli utenti interagiscono con le scene, fornendo un feedback immediato.
Applicazioni Educative
NablaVis può essere utilizzato in vari contesti educativi:
- Dimostrazioni in aula: Gli insegnanti possono utilizzare lo strumento durante le lezioni per illustrare i concetti del calcolo vettoriale con esempi dal vivo e interattivi
- Esplorazione degli studenti: Gli studenti possono sperimentare con diversi campi e percorsi per costruire l'intuizione sui teoremi
- Verifica dei compiti: La conferma visiva e numerica aiuta gli studenti a verificare la loro comprensione dei problemi
- Studio autonomo: La natura interattiva lo rende adatto per l'apprendimento indipendente al di fuori dell'aula
Prova NablaVis
Prova NablaVis direttamente nel tuo browser:
Avvia NablaVis
L'applicazione non richiede installazione e funziona su qualsiasi browser web moderno con supporto WebGL.
Per la migliore esperienza, utilizza una versione recente di Chrome, Firefox, Safari o Edge.
Sviluppo e Contributi
NablaVis è stato sviluppato utilizzando l'assistenza AI (Gemini con Antigravity) come parte di un'esplorazione nello sviluppo software assistito da AI per strumenti educativi.
Il progetto segue le pratiche standard di sviluppo TypeScript e JavaScript moderno:
Clonare il repository:
git clone https://github.com/ettoremessina/NablaVis.git
cd NablaVisInstallare le dipendenze:
npm installAvviare il server di sviluppo:
npm run devBuild per la produzione:
npm run builddist/ e può essere distribuito su qualsiasi servizio di hosting statico.
Codice Sorgente e Licenza
Il codice sorgente completo è disponibile su GitHub a questo indirizzo: NablaVis.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.