$\newcommand{\dee}{\mathop{\mathrm{d}\!}}$

Esperimenti con SymPy per risolvere equazioni differenziali ordinarie del 1° ordine

Questo sito web si occupa principalmente di computazione numerica e in altri post in cui si è trattato l'argomento delle equazioni differenziali si sono proposte infatti soluzioni numeriche opportune (si veda Risolutori di equazioni differenziali ordinarie in Python); tuttavia quando è possibile determinare una soluzione analitica sarebbe in generale da preferirla a quella numerica sia perché essa è esatta (e non approssimata) che anche per motivi di performance. Nell'ecosistema di Python vi è la libreria SymPy che è una libreria di matematica simbolica e il suo obiettivo è quello di essere un sistema di algebra computerizzata completa (CAS).
Questo post mostra come utilizzare SymPy per risolvere analiticamente equazioni differenziali ordinarie (abbreviato ODE da Ordinary Differential Equation) in Python e inoltre con la "lambdificazione" si mostra come passare dalla rappresentazione simbolica a un oggeto Python "callable" e quindi eseguire calcoli numerici a partire da soluzioni analitiche esatte.

Tutti gli esempi di questo post e le relative soluzioni sono stati forniti dalla prof.ssa Fausta D'Acunzo di Preparazione 2.0: ogni esempio cade in una qualche tipologia nota di ODE del primo ordine e per ciascun esempio verrà confrontata la soluzione corretta, calcolata a mano da Preparazione 2.0, e quella ottenuta dalla libreria SymPy.

Installare e usare SymPy

Per installare SymPy con pip è sufficiente eseguire: 

$ pip install sympy
Per installare con conda su Anaconda eseguire:

$ conda install sympy
È anche possibile installare SymPy dai sorgenti o con altri metodi; si veda docs.sympy.org/latest/install.html per dettagli.

SymPy è anche disponibile online all'indirizzo live.sympy.org, quindi senza necessità di doverlo installare localmente. Se ci si serve della versione online si tenga presente che i seguenti import sono pre-eseguiti:

from __future__ import division
from sympy import *
x, y, z, t = symbols('x y z t')
k, m, n = symbols('k m n', integer=True)
f, g, h = symbols('f g h', cls=Function)
Tutti i vari frammenti di codice descritti in questo post richiedono la versione 3.x di Python, ovviamente il package SymPy e i seguenti package: NumPy, MatPlotLib.
Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.

Convenzioni

In questo post le convenzioni adoperate sono le seguenti:

  • $t$ è la variabile indipendente
  • $f$ è la funzione incognita
  • $f$ è da intendersi funzione di $t$, quindi $f=f(t)$
  • $f'$ è la derivata prima di f rispetto a $t$ nella notazione di Lagrange
  • $\frac{\dee f(t)}{\dee t}$ è la derivata prima di f rispetto a $t$ nella notazione di Leibniz


ODE a variabili separabili (primo esempio)

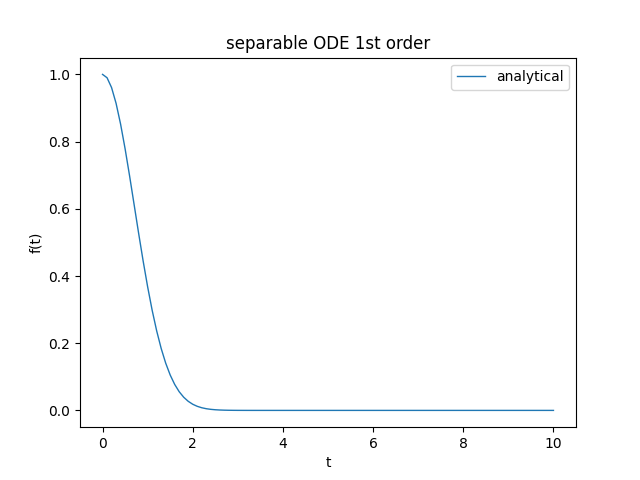
Sia dato il seguente problema di Cauchy: $$ \begin{equation} \begin{cases} f' = -2 \mkern3mu t \mkern3mu f \\ f(0) = 1 \end{cases} \end{equation} $$ che riscritto in notazione di Leibniz (che è quella utilizzata da SymPy) diventa: $$ \begin{equation} \begin{cases} \frac{\dee f(t)}{\dee t} = -2 \mkern3mu t \mkern3mu f(t) \\ f(0) = 1 \end{cases} \end{equation} $$ la cui soluzione esatta, fornita da Preparazione 2.0, è: $$f(t) = e^{-t^2}$$ Con SymPy l'equazione di cui sopra si dichiara nel seguente modo: 

eq = Eq(f(t).diff(t), -2 * t * f(t))
print('ODE class: ', classify_ode(eq)[0])
il cui output è:

ODE class: separable
da cui si evince chiaramente che la classe di ODE determinata dalla libreria è quella attesa.

Per risolvere il problema di Cauchy proposto eseguire il seguente statement Python:

an_sol = dsolve(eq, ics={f(0): 1})
pprint(an_sol)
il cui output è:

           2
        -t 
f(t) = e
da cui si evince chiaramente che la soluzione ottenuta dalla libreria è quella attesa.

Per passare dal calcolo simbolico al calcolo numerico bisogna effettuare una "lambdificazione" della parte destra della soluzione:

lmbd_sol = lambdify(t, an_sol.rhs)
ed eseguendo questo semplicissimo test:

t_range = [0., 0.5, 1., 1.5, 2.0]
print([lmbd_sol(ti) for ti in t_range])
il cui output è:

[1.0,
0.7788007830714049, 
0.36787944117144233, 
0.10539922456186433, 
0.01831563888873418]
si vede chiaramente che dal risultato simbolico si è passati al risultato numerico.

Qui il link al codice su GitHub.

Grafico della funzione $f(t)$, soluzione del precedente problema di Cauchy.


ODE a variabili separabili (secondo esempio)

Sia dato il seguente problema di Cauchy: $$ \begin{equation} \begin{cases} f' = \frac{t-1}{f + 1} \\ f(0) = 0 \end{cases} \end{equation} $$ che riscritto in notazione di Leibniz (che è quella utilizzata da SymPy) diventa: $$ \begin{equation} \begin{cases} \frac{\dee f(t)}{\dee t} = \frac{t-1}{f(t) + 1} \\ f(0) = 0 \end{cases} \end{equation} $$ la cui soluzione esatta, fornita da Preparazione 2.0, è: $$f(t) = -t$$ Con SymPy l'equazione di cui sopra si dichiara nel seguente modo: 

eq = Eq(f(t).diff(t), (t-1)/(f(t)+1))
print('ODE class: ', classify_ode(eq)[0])
il cui output è:

ODE class:  separable
da cui si evince chiaramente che la classe di ODE determinata dalla libreria è quella attesa.

Per risolvere il problema di Cauchy proposto eseguire il seguente statement Python:

an_sol = dsolve(eq, ics={f(0): 0})
pprint(an_sol)
il cui output è:

          ______________    
         ╱  2               
f(t) = ╲╱  t  - 2⋅t + 1  - 1
La soluzione ottenuta sembra diversa da quella fornita, tuttavia si osservi che il valore sotto radice è il quadrato del binomio $(t-1)$ e il quadrato si elide con la radice per cui semplificando la soluzione diventa $f(t)=|t-1| - 1$ e togliendo il modulo si ottengono le due possibili soluzioni $f(t)=t-2$ e $f(t)=-t$ e considerando la condizione di Cauchy $f(0)=0$, la soluzione trovata è $f(t)=-t$ è esattamente quella prevista.

Il passaggio dal calcolo simbolico a quello numerico e il tracciamento del grafico sono praticamente identici al caso precedente e si rimanda al codice per i dettagli.

Qui il link al codice su GitHub.

ODE omogenea

Sia dato il seguente problema di Cauchy: $$ \begin{equation} \begin{cases} f' = \frac{t^2+f^2}{tf} \\ f(2) = 2 \end{cases} \end{equation} $$ che riscritto in notazione di Leibniz (che è quella utilizzata da SymPy) diventa: $$ \begin{equation} \begin{cases} \frac{\dee f(t)}{\dee t} = \frac{t^2+f(t)^2}{tf(t)} \\ f(2) = 2 \end{cases} \end{equation} $$ la cui soluzione esatta, fornita da Preparazione 2.0, è: $$f(t) = t \sqrt{2 \ln{\frac{t}{2}} + 1} $$ Con SymPy l'equazione di cui sopra si dichiara nel seguente modo: 

eq = Eq(f(t).diff(t), (t**2 + f(t)**2)/(t * f(t)))
print('ODE class: ', classify_ode(eq)[0])
il cui output è:

ODE class:  Bernoulli
da cui si vede che la libreria sceglie di risolvere l'equazione usando una classe di ODE diversa da quella attesa.

Per risolvere il problema di Cauchy proposto, forzando la libreria a usare la classe desiderata, eseguire il seguente statement Python:

an_sol = dsolve(eq, hint='1st_homogeneous_coeff_best', ics={f(2):2})
pprint(an_sol)
il cui output è:

            ______________________
           ╱    ⎛ 2⎞              
f(t) = t⋅╲╱  log⎝t ⎠ - log(4) + 1
La soluzione ottenuta sembra diversa da quella fornita, tuttavia si osservi che i valori sotto radice sono equivalenti per le proprietà dei logaritmi (precisamente entrambe equivalgono a $1 + \ln {\frac{t^2}{4}}$) e quindi la soluzione trovata è esattamente quella prevista.

Il passaggio dal calcolo simbolico a quello numerico e il tracciamento del grafico sono praticamente identici al primo caso precedente e si rimanda al codice per i dettagli.

Qui il link al codice su GitHub.

ODE lineare (primo esempio)

Sia dato il seguente problema di Cauchy: $$ \begin{equation} \begin{cases} f' = 3 \mkern3mu t^2 \mkern3mu f + t \mkern3mu e^{t^3} \\ f(0) = 1 \end{cases} \end{equation} $$ che riscritto in notazione di Leibniz (che è quella utilizzata da SymPy) diventa: $$ \begin{equation} \begin{cases} \frac{\dee f(t)}{\dee t} = 3 \mkern3mu t^2 \mkern3mu f(t) + t \mkern3mu e^{t^3} \\ f(0) = 1 \end{cases} \end{equation} $$ la cui soluzione esatta, fornita da Preparazione 2.0, è: $$f(t) = (\frac{t^2}{2} + 1) \mkern3mu e^{t^3}$$ Con SymPy l'equazione di cui sopra si dichiara nel seguente modo: 

eq = Eq(f(t).diff(t), 3 * t**2 * f(t) + t * exp(t**3))
print('ODE class: ', classify_ode(eq)[0])
il cui output è:

ODE class: 1st_exact
da cui si vede che la libreria sceglie di risolvere l'equazione usando una classe di ODE diversa da quella attesa.

Per risolvere il problema di Cauchy proposto, forzando la libreria a usare la classe desiderata, eseguire il seguente statement Python:

an_sol = dsolve(eq, hint='1st_linear', ics={f(0): 1})
pprint(an_sol)
il cui output è:

       / 2    \  / 3\
       |t     |  \t /
f(t) = |-- + 1|*e    
       \2     /
La soluzione ottenuta è esattamente quella prevista.

Il passaggio dal calcolo simbolico a quello numerico e il tracciamento del grafico sono praticamente identici al primo caso precedente e si rimanda al codice per i dettagli.

Qui il link al codice su GitHub.

ODE lineare (secondo esempio)

Sia dato il seguente problema di Cauchy: $$ \begin{equation} \begin{cases} f' = \frac{t}{1 + t^2} \mkern3mu f + 1 \\ f(0) = 0 \end{cases} \end{equation} $$ che riscritto in notazione di Leibniz (che è quella utilizzata da SymPy) diventa: $$ \begin{equation} \begin{cases} \frac{\dee f(t)}{\dee t} = \frac{t}{1 + t^2} \mkern3mu f(t) + 1 \\ f(0) = 0 \end{cases} \end{equation} $$ la cui soluzione esatta, fornita da Preparazione 2.0, è: $$f(t) = \sqrt{1 + t^2} \ln(t + \sqrt{1 + t^2})$$ Con SymPy l'equazione di cui sopra si dichiara nel seguente modo: 

eq = Eq(f(t).diff(t), (t / (1 + t**2)) * f(t) + 1)
print('ODE class: ', classify_ode(eq)[0])
il cui output è:

ODE class: 1st_exact
da cui si vede che la libreria sceglie di risolvere l'equazione usando una classe di ODE diversa da quella attesa.

Per risolvere il problema di Cauchy proposto, forzando la libreria a usare la classe desiderata, eseguire il seguente statement Python:

an_sol = dsolve(eq, hint='1st_linear', ics={f(0): 0})
pprint(an_sol)
il cui output è:

        2                    
       t *asinh(t) + asinh(t)
f(t) = ----------------------
               ________      
              /  2           
            \/  t  + 1
La soluzione sembrerebbe diversa da quella attesa, ma in realtà, applicando le definizioni di $arcsinh$ e $arccosh$ si ottiene lo stesso risultato.
La prova nel grafico delle sue soluzioni come mostrato in figura.

Qui il link al codice su GitHub.

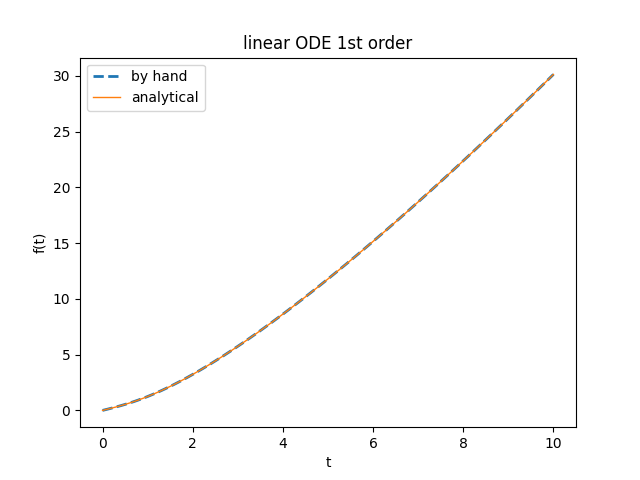
Grafici della funzione $f(t)$, soluzione del precedente problema di Cauchy
calcolato con la formula attesa e con quella ottenuta dalla libreria e sono naturalmente identici.


Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.