Approssimazione di funzioni tramite PyCaret

Questo post tratta l'approssimazione di funzioni matematiche reali scalari a una o più variabili reali tramite PyCaret senza scrivere codice ma agendo solo sulla linea di comando di script Python che implementano le funzionalità di:

Il codice descritto da questo post richiede la versione 3 di Python e utilizza la libreria PyCaret; richiede inoltre le librerie NumPy, Pandas e MatPlotLib. Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.

Per quanto riguarda la generazione dei dataset sintetici di training e di test si farà uso dei seguenti strumenti (presenti nel repository):
  • fx_gen.py per le funzioni generatrici scalari reali di una variabile reale $f(x) \colon [a,b] \to {\rm I\!R}$
  • fxy_gen.py per le funzioni generatrici scalari reali di due variabili reali $f(x,y) \colon [a,b] \times [c,d] \to {\rm I\!R}$
Per la visualizzazione dei risultati, e precisamente per la comparazione del dataset di test con la predizione, si farà uso dei seguenti strumenti (sempre presenti nel repository):
  • fx_scatter.py per le funzioni scalari reali di una variabile reale
  • fxy_scatter.py per le funzioni scalari reali di due variabili reali

Configurazione di parametri generali del regressore di PyCaret e addestramento

In questo capitolo viene presentato il programma: fit_func.py che implementa in sequenza cinque chiamate ad altrettante funzioni della libreria PyCaret:

  • regression.setup che inizializza l'ambiente di addestramento e crea la pipeline di trasformazione.
  • regression.compare_models che addestra e valuta le performance di tutti gli estimatori disponibili nella libreria dei modelli utilizzando la validazione incrociata.
    Nota: compare_models in generale restituisce una griglia di punteggi medi dei vari estimatori convalidati in modo incrociato; il programma fit_func.py comunque utilizzerà l'estimatore che ha performato meglio, cioè quello che sta nella prima riga della griglia.
  • regression.tune_model che mette a punto gli iperparametri di un dato estimatore; il programma fit_func.py applicherà tune_model sul migliore estimatore trovato da compare_models al punto precedente.
  • regression.finalize_model che addestra un dato estimatore sull'intero set di dati; il programma fit_func.py applicherà finalize_model all'estimatore restituito tune_model al punto precedente.
  • regression.save_model salva la pipeline di trasformazione e l'oggetto modello addestrato su un file in formato pickle per l'uso successivo da parte di predict_func.py.
Il fine di questo programma è di eseguire la sequenza di comandi ci cui sopra per consentire a PyCaret di scegliere il miglior algoritmo di machine learning per effettuare la regressione per approssimare funzioni senza dover scrivere codice ma agendo solo sulla linea di comando.
Infatti tramite l'argomento --setupparams l'utente passa una serie di iperparametri per configurare la regressione di PyCaret e tramite l'argomento --compareparams invece l'utente passa una serie di iperparametri alla comparazione tra gli algoritmi effettuata da PyCaret. Oltre agli iperparametri della libreria PyCaret sottostante, il programma supporta dei propri argomenti per consentire all'utente di passare il dataset di training e il file ove salvare il modello addestrato.

Il programmi ` di tipo M.I.S.O., cioè Multiple Input Simple Output: è progettato per approssimare una funzione della forma $f \colon \rm I\!R^n \to \rm I\!R$.
Il formato dei dataset in ingresso è in formato csv (con header); una di queste colonne (indicata tramite un argomento obbligatorio della lina di comando) è la colonna target (quella relativa alla variabile dipendente) mentre tutte le altre colonne contengono i valori delle variabili indipendenti.

Usage del programma fit_func.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python fit_func.py --help
e l'output ottenuto è: 

usage: fit_func.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                   --targetcol TARGET_COLUMN --modelout MODEL_FILE
                   [--metric METRIC] [--setupparams SETUP_PARAMS]
                   [--compareparams COMPARE_PARAMS]

fit_func.py fits a multiple-input single-output function dataset using the
best regressor chosen by PyCaret

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --targetcol TARGET_COLUMN
                        Target column name
  --modelout MODEL_FILE
                        Output model file
  --metric METRIC       metric to evaluate the best model
  --setupparams SETUP_PARAMS
                        Parameters of PyCaret regression.setup function
  --compareparams COMPARE_PARAMS
                        Parameters of PyCaret regression.compare_models
                        function
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --trainds: percorso (relativo o assoluto) del file csv (con header) che contiene il dataset da utilizzare per il training; questo file può essere generato in modo sintetico ad esempio tramite uno dei programmi di cui sopra oppure essere un dataset del mondo reale che mappa $n$ variabili indipendenti su $1$ variabile dipendente.

  • --targetcol: nome della colonna che rappresenta la variabile dipendente.

  • --modelout: percorso (relativo o assoluto) al file dove salvare il modello addestrato nel formato pickle.

  • --metric: la metrica da utilizzare nell'ordinamento della griglia dei punteggi. I valori ammessi sono: MAE, MSE, RMSE, R2, RMSLE, MAPE; il default è R2.

  • --setupparams: lista di parametri da passare alla funzione regression.setup sottostante; si veda la documentazione di regression.setup.

  • --compareparams: lista di parametri da passare alla funzione regression.compare_models sottostante; si veda la documentazione di regression.compare_models

Predizione e calcolo dell'errore

In questo capitolo viene invece presentato il programma predict_func.py il cui scopo è quello di effettuare le predizioni su un dataset di test applicandolo al modello precedentemente selezionato e addestrato da PyCaret tramite il programma fit_func.py sempre senza dover scrivere codice ma tramite la sola linea di comando.
Infatti tale programma supporta argomenti tramite i quali l'utente passa il modello selezionato e addestrato precentemente, il dataset di test e le misure di errore da calcolare tra la predizione e il valore vero.
Il formato dei dataset di test in ingresso è identico a quello del programma di training di cui sopra; ovviamente qui la colonna target (quella della variabile dipendente) è adoperata solo per confrontare i valori predetti con i valori veri calcolando le misure di errore passate.

Usage del programma predict_func.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python predict_func.py --help
e l'output ottenuto è: 

usage: predict_func.py [-h] [--version] --model MODEL_FILE --ds DF_PREDICTION
                       --targetcol TARGET_COLUMN --predictionout
                       PREDICTION_DATA_FILE
                       [--measures MEASURES [MEASURES ...]]

predict_func.py makes prediction of the values of a multiple-input single-
output function with the best pretrained regressor chosen by PyCaret

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --model MODEL_FILE    model file
  --ds DF_PREDICTION    dataset file (csv format)
  --targetcol TARGET_COLUMN
                        Target column name
  --predictionout PREDICTION_DATA_FILE
                        prediction data file (csv format)
  --measures MEASURES [MEASURES ...]
                        List of built-in sklearn regression measures to
                        compare prediction with input dataset
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --model: percorso (relativo o assoluto) al file nel formato pickle del modello selezionato e addestrato da PyCaret e generato dal programma di training sopra descritto.

  • --ds: percorso (relativo o assoluto) del file csv (con header) che contiene il dataset di input su cui calcolare la predizione.

  • --targetcol: nome della colonna che rappresenta la variabile dipendente.

  • --predictionout: percorso (relativo o assoluto) del file csv da generare che conterrà la predizione, ovverosia l'approssimazione della funzione applicata al dataset di input.

  • --measures: lista di misure da calcolare confrontando i valori veri del dataset di input e i valori predetti in uscita; la lista delle metriche supportate è definita in SciKit Learn Regression Metrics.

Esempi di approssimazione di funzione scalare reale di una variabile reale

Esempio #1

Si supponga di voler approssimare nell'intervallo $[-10,10]$ la seguente funzione $$f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$$ Questa si traduce in sintassi lambda body Python così: 

0.5*x**3 - 2*x**2 - 3*x - 1
Per generare il dataset di training, tramite il programma fx_gen.py, si esegua quindi il seguente comando: 

$ python fx_gen.py \
  --dsout mytrain.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.01
mentre per generare il dataset di test, si esegua il seguente comando: 

$ python fx_gen.py \
  --dsout mytest.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.0475
Si osservi che il passo di discretizzazione del dataset di test è più grande di quello di training e questo è normale in quanto l'addestramento, per essere accurato, deve essere eseguito su una maggiore quantità di dati. Inoltre si osservi che è opportuno che il passo di discretizzazione del dataset di test non sia un multiplo di quello di training per garantire che il dataset di test contenga la maggior parte dei dati non presenti nel dataset di training, e questo rende più interessante la predizione.

A questo si intende effettuare una regressione tramite fit_func.py passando al regressore sottostante i seguenti argomenti: 'train_size': 0.8, 'session_id': 987654321, 'log_experiment': True, 'experiment_name': 'example1_pycaret'; quindi si esegua quindi il seguente comando: 

$ python fit_func.py \
  --trainds mytrain.csv \
  --targetcol y \
  --metric MAE \
  --modelout mymodel.pickle \
  --setupparams "'train_size': 0.8, 'session_id': 987654321,
    'log_experiment': True, 'experiment_name': 'example1_pycaret'"
e alla fine dell'esecuzione il programma mostra il migliore algoritmo di regressione selezionato da PyCaret, che è in questo esperimento ExtraTreesRegressor, e salva il file mymodel.pickle che contiene il modello del regressore selezionato, configurato e addestrato.

Adesso si intende effettuare la predizione e il calcolo dell'errore usando le misure mean_absolute_error e mean_squared_error tramite predict_func.py; quindi si esegua quindi il seguente comando: 

$ python predict_func.py \
  --model mymodel.pickle \
  --ds mytest.csv \
  --targetcol y \
  --predictionout mypred.csv \
  --measures mean_absolute_error mean_squared_error
e alla fine dell'esecuzione il file mypred.csv salvato contiene la predizione eseguita applicando il modello sui dati di test; l'output del programma visualizza le misure di errore passate tramite l'argomento --measures e sono molto basse: la prima intorno a $0.0161$ e la seconda intorno a $0.002$

Infine si intende effettuare la visualizzazione comparata del dataset di test con la predizione tramite fx_scatter.py; si esegua perciò il seguente comando: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --xlabel "x" \
  --ylabel "y=1/2 x^3 - 2x^2 - 3x - 1"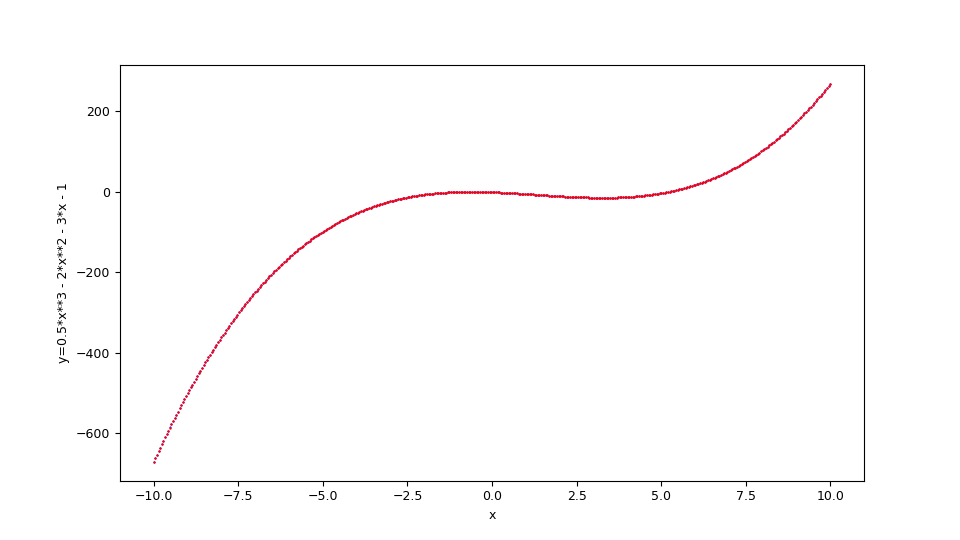
che mostra i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Confronto del grafico tra funzione originale e la funzione approssimata dal regressore selezionato e addestrato da PyCaret
Figura con grafici a dispersione che mostra l'approssimazione in sovraimpressione in rosso della funzione
$f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$ e la funzione originale sottostante in blu.


Lo script shell di questo esempio (che mostra l'uso in cascata di questi programmi) al seguente url:
one-variable-function/pycaret/examples/example1.sh.

Esempio #2

Si supponga di voler approssimare nell'intervallo $[-6,6]$ la seguente funzione $$f(x)=\sin x $$ Tenendo presente che np è l'alias della libreria NumPy, questa si traduce in sintassi lambda body Python così: 

np.sin(x)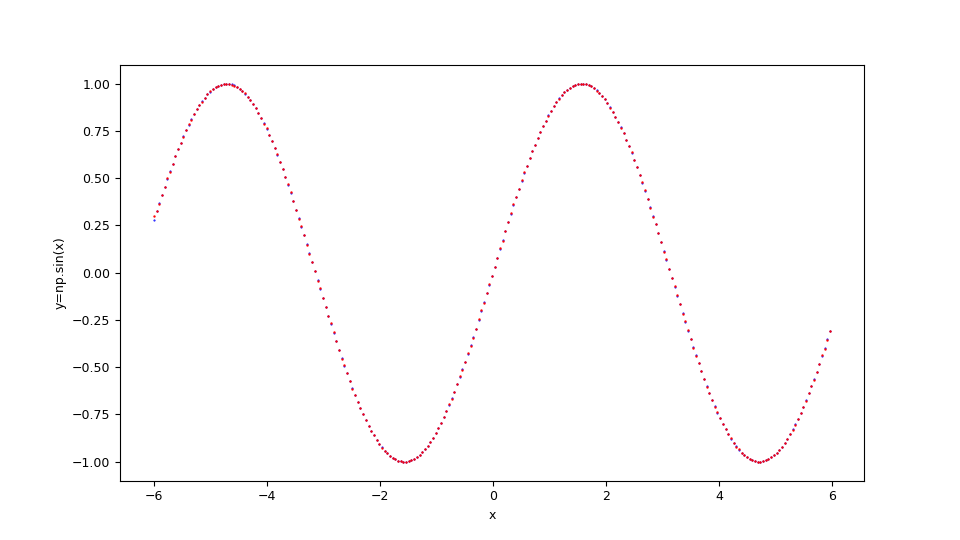
Eseguendo gli stessi passi dell'esempio precedente, alla fine vengono mostrati i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Confronto del grafico tra funzione originale e la funzione approssimata dal regressore selezionato e addestrato da PyCaret
Figura con grafici a dispersione che mostra l'approssimazione in sovraimpressione in rosso della funzione
$f(x)=\sin x $ e la funzione originale sottostante in blu.


Lo script shell di questo esempio (che mostra l'uso in cascata di questi programmi) al seguente url:
one-variable-function/pycaret/examples/example2.sh.

Esempio #3

Si supponga di voler approssimare nell'intervallo $[-8,8]$ la seguente funzione $$f(x)=e^{\sin x}$$ Tenendo presente che np è l'alias della libreria NumPy, questa si traduce in sintassi lambda body Python così: 

np.exp(np.sin(x))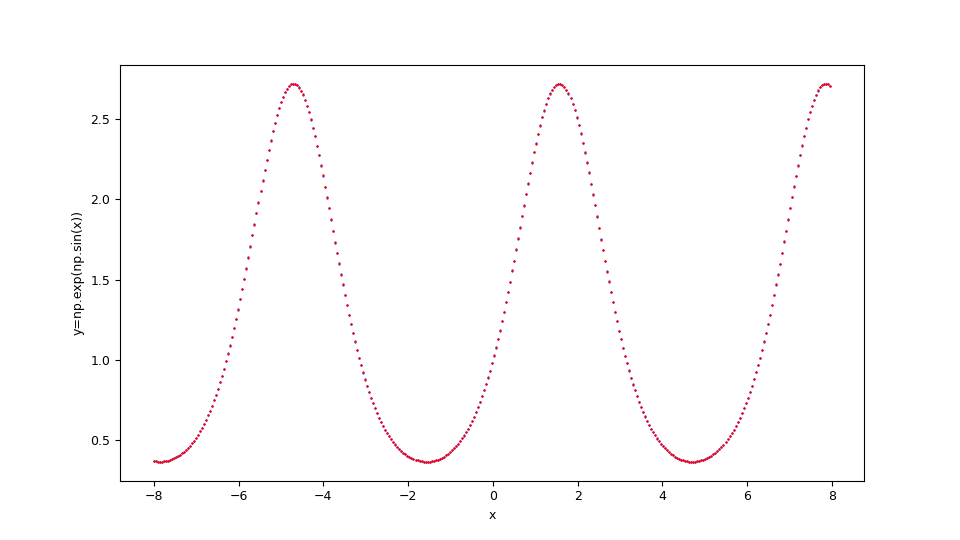
Eseguendo gli stessi passi dell'esempio precedente, alla fine vengono mostrati i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Confronto del grafico tra funzione originale e la funzione approssimata dal regressore selezionato e addestrato da PyCaret
Figura con grafici a dispersione che mostra l'approssimazione in sovraimpressione in rosso della funzione
$f(x)=e^{\sin x}$ e la funzione originale sottostante in blu.


Lo script shell di questo esempio (che mostra l'uso in cascata di questi programmi) al seguente url:
one-variable-function/pycaret/examples/example3.sh.

Esempi di approssimazione di funzione scalare reale di due variabile reali

Esempio #1

Si supponga di voler approssimare nell'insieme $[-3,3] \times [-3,3]$ la seguente funzione $$f(x,y)=x^2 + y^2$$ Questa si traduce in sintassi lambda body Python così: 

x**2 + y**2
Per generare il dataset di training, tramite il programma fxy_gen.py, si esegua quindi il seguente comando: 

$ python fxy_gen.py \
  --dsout mytrain.csv \
  --funcxy "x**2 + y**2" \
  --xbegin -3.0 --xend 3.0 \
  --ybegin -3.0 --yend 3.0 \
  --xstep 0.05 --ystep 0.1
mentre per generare il dataset di test, si esegua il seguente comando: 

$ python fyx_gen.py \
  --dsout mytest.csv \
  --funcxy "x**2 + y**2" \
  --xbegin -3.0 --xend 3.0 \
  --ybegin -3.0 --yend 3.0 \
  --xstep 0.0875 --ystep 0.5
Si osservi che il passo di discretizzazione del dataset di test è più grande di quello di training e questo è normale in quanto l'addestramento, per essere accurato, deve essere eseguito su una maggiore quantità di dati. Inoltre si osservi che è opportuno che il passo di discretizzazione del dataset di test non sia un multiplo di quello di training per garantire che il dataset di test contenga la maggior parte dei dati non presenti nel dataset di training, e questo rende più interessante la predizione.

A questo si intende effettuare una regressione tramite fit_func.py passando al regressore sottostante i seguenti argomenti: 'train_size': 0.8, 'session_id': 987654321, 'log_experiment': True, 'experiment_name': 'example1_pycaret'; quindi si esegua quindi il seguente comando: 

$ python fit_func.py \
  --trainds mytrain.csv \
  --targetcol z \
  --metric MAE \
  --modelout mymodel.pickle \
  --setupparams "'train_size': 0.8, 'session_id': 987654321,
    'log_experiment': True, 'experiment_name': 'example1_pycaret'"
e alla fine dell'esecuzione il programma mostra il migliore algoritmo di regressione selezionato da PyCaret, che è in questo esperimento ExtraTreesRegressor, e salva il file mymodel.pickle che contiene il modello del regressore selezionato, configurato e addestrato.

Adesso si intende effettuare la predizione e il calcolo dell'errore usando le misure mean_absolute_error e mean_squared_error tramite predict_func.py; quindi si esegua quindi il seguente comando: 

$ python predict_func.py \
  --model mymodel.pickle \
  --ds mytest.csv \
  --targetcol z \
  --predictionout mypred.csv \
  --measures mean_absolute_error mean_squared_error
e alla fine dell'esecuzione il file mypred.csv salvato contiene la predizione eseguita applicando il modello sui dati di test; l'output del programma visualizza le misure di errore passate tramite l'argomento --measures e sono molto basse: la prima intorno a $0.00389864$ e la seconda intorno a $0.00004255$

Infine si intende effettuare la visualizzazione comparata del dataset di test con la predizione tramite fxy_scatter.py; si esegua perciò il seguente comando: 

$ python fxy_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --xlabel "x" \
  --ylabel "y" \
  --zlabel "z=x**2 + y**2"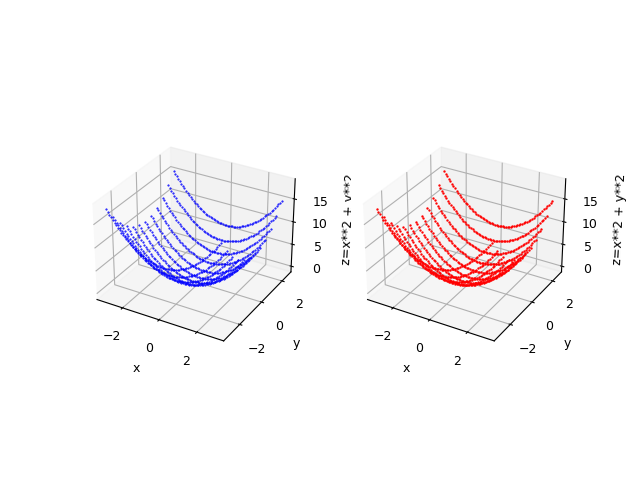
che mostra accanto i grafici a dispersione del dataset di test e la predizione: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Confronto del grafico tra funzione originale e la funzione approssimata dal regressore selezionato e addestrato da PyCaret
Figura con grafici a dispersione che mostra accanto l'approssimazione in rosso della funzione
$f(x,y)=x^2 + y^2$ e la funzione originale in blu.


Lo script shell di questo esempio (che mostra l'uso in cascata di questi programmi) al seguente url:
two-variables-function/pycaret/examples/example1.sh.

Esempio #2

Si supponga di voler approssimare nell'insieme $[-5,5] \times [-5,5]$ la seguente funzione $$f(x,y)=\sin \sqrt{x^2 + y^2}$$ Tenendo presente che np è l'alias della libreria NumPy, questa si traduce in sintassi lambda body Python così: 

np.sin(np.sqrt(x**2 + y**2))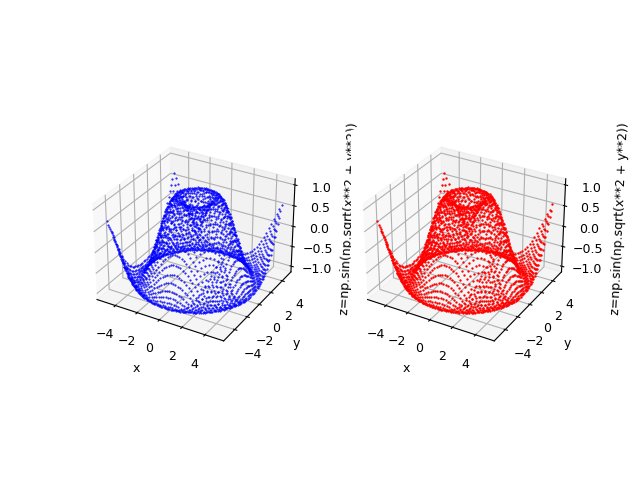
Eseguendo gli stessi passi dell'esempio precedente, alla fine vengono mostrati i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Confronto del grafico tra funzione originale e la funzione approssimata dal regressore selezionato e addestrato da PyCaret
Figura con grafici a dispersione che mostra accanto l'approssimazione in rosso della funzione
$f(x,y)=\sin \sqrt{x^2 + y^2}$ e la funzione originale in blu.


Lo script shell di questo esempio (che mostra l'uso in cascata di questi programmi) al seguente url:
two-variables-function/pycaret/examples/example2.sh.

Citazioni

@ManualPyCaret,
  author  = {Moez Ali},
  title   = {PyCaret: An open source, low-code machine learning library in Python},
  year    = {2020},
  month   = {April},
  note    = {PyCaret version 1.0.0},
  url     = {https://www.pycaret.org}

Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.