Approssimazione di funzioni tramite un regressore XGBoost configurabile

Questo post tratta dell'approssimazione di funzioni matematiche, sia scalari che vettoriali, sia a una che più variabili reali tramite un regressore XGBoost senza scrivere codice ma agendo solamente sulla linea di comando di script Python che implementano le funzionalità di:

  • Configurazione del regressore e addestramento
  • Predizione e calcolo dell'errore
Il codice descritto da questo post richiede la versione 3 di Python e utilizza la libreria XGBoost; richiede inoltre le librerie SciKit-Learn, NumPy, Pandas, MatPlotLib e JobLib. Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.

Per quanto riguarda la generazione dei dataset sintetici di training e di test si farà uso dei seguenti strumenti (presenti nel repository):
  • fx_gen.py per le funzioni generatrici scalari reali di una variabile reale $f(x) \colon [a,b] \to {\rm I\!R}$
  • fxy_gen.py per le funzioni generatrici scalari reali di due variabili reali $f(x,y) \colon [a,b] \times [c,d] \to {\rm I\!R}$
  • pcm2t_gen.py per le curve parametriche sul piano, quindi funzioni vettoriali reali $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R}$
  • pmc3t_gen.py per le curve parametriche nello spazio, quindi funzioni vettoriali reali $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R \times \rm I\!R}$
Per la visualizzazione dei risultati, e precisamente per la comparazione del dataset di test con la predizione, si farà uso dei seguenti strumenti (sempre presenti nel repository):

Configurazione del regressore e addestramento

In questo capitolo sono presentati i programmi fit_func_miso.py e fit_func_mimo.py che sono tecnicamente wrapper della classe XGBRFRegressor della libreria XGBoost e il cui fine è di consentire l'utilizzazione del regressore sottostante per approssimare funzioni senza dover scrivere codice ma agendo solo sulla linea di comando.
Infatti tramite l'argomento --xgbparams l'utente passa una serie di iper parametri per regolare il comportamento dell'algoritmo del regressore XGBoost sottostante e altri per configurare l'apprendimento dello stesso. Oltre ai parametri del regressore sottostante i due programmi supportano dei propri argomenti per permettere all'utente di passare il dataset di training ed eventualmente quello di validazione, su quale file salvare il modello addestrato, le metriche da calcolare durante il training, vincoli per la regolarizzazione (ad esempio l'early stop) e parametrri per la diagnostica.

Il programma fit_func_miso.py, così come il regressore XGBoost sottostante, è di tipo M.I.S.O., cioè Multiple Input Single Output: è progettato per approssimare una funzione scalre della forma $f \colon \rm I\!R^n \to \rm I\!R$ dove il numero delle variabili indipendenti è arbitrariamente grande mentre la variabile dipendete in uscita è solamente una.
Il formato dei dataset in ingresso è in formato csv (con header), con n + 1 colonne, di cui le prime n contengono i valori delle n variabili indipendenti e l'ultima colonna, la n+1, contenente i valori della variabile dipendente.
Il programma fit_func_mimo.py, utilizzando nell'implementazione la classe sklearn.multioutput.MultiOutputRegressor è di tipo M.I.M.O., cioè Multiple Input Multiple Output: è progettato per approssimare una funzione vettoriale della forma $f \colon \rm I\!R^n \to \rm I\!R^m$ dove il numero delle variabili indipendenti è arbitrariamente grande mentre la variabile dipendete in uscita è solamente una.
Il formato dei dataset in ingresso è in formato csv (con header), con $n + m$ colonne, di cui le prime $n$ colonne contengono i valori delle $n$ variabili indipendenti e le ultime $m$ contenenti i valori delle variabili dipendenti.

Usage del programma fit_func_miso.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python fit_func_miso.py --help
e l'output ottenuto è: 

usage: fit_func_miso.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                        --modelout MODEL_FILE [--valds VAL_DATASET_FILENAME]
                        [--metrics VAL_METRICS [VAL_METRICS ...]]
                        [--dumpout DUMPOUT_PATH]
                        [--earlystop EARLY_STOPPING_ROUNDS]
                        [--xgbparams XGB_PARAMS]

fit_func_miso.py fits a multiple-input single-output scalar function dataset
using a configurable XGBoost

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --modelout MODEL_FILE
                        Output model file
  --valds VAL_DATASET_FILENAME
                        Validation dataset file (csv format)
  --metrics VAL_METRICS [VAL_METRICS ...]
                        List of built-in evaluation metrics to apply to
                        validation dataset
  --dumpout DUMPOUT_PATH
                        Dump directory (directory to store metric values)
  --earlystop EARLY_STOPPING_ROUNDS
                        Number of round for early stopping
  --xgbparams XGB_PARAMS
                        Parameters of XGBoost constructor
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --trainds: percorso (relativo o assoluto) del file csv a due colonne (con header) che contiene il dataset da utilizzare per il training; questo file può essere generato in modo sintetico ad esempio tramite il programma fx_gen.py oppure essere un dataset ottenuto realmente misurando un fenomeno scalare e reale che dipende da una sola variabile reale.

  • --modelout: percorso (relativo o assoluto) al file dove salvare il modello addestrato nel formato joblib (.jl).

  • --valds: percorso (relativo o assoluto) del file csv a due colonne (con header) che contiene il dataset da utilizzare per il validation.

  • --metrics: lista di metriche da calcolare sul dataset di training e, se presente, anche su quello di validation; la lista delle metriche supportate è definita in XGBoost Parameters alla voce eval_metric.

  • --dumpout: percorso (relativo o assoluto) della directory dove salvare i valori delle metriche allo scorrere delle epoche; il programma dumps_scatter.py utilizzerà il contenuto di questa directory per visualizzare i grafici delle metriche.

  • --earlystop: quante iterazioni possono essere eseguite prima che l'algoritmo inizi a entrare nella fase di overfitting.

  • --xgbparams: lista di parametri da passare all'algoritmo di regressione di XGBoost; si veda la documentazione di XGBRegressor.

Usage del programma fit_func_mimo.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python fit_func_mimo.py --help
e l'output ottenuto è: 

usage: fit_func_mimo.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                        --outputdim NUM_OF_DEPENDENT_COLUMNS --modelout
                        MODEL_FILE [--dumpout DUMPOUT_PATH]
                        [--xgbparams XGB_PARAMS]

fit_func_mimo.py fits a multiple-input single-output (scalar) function dataset
using a configurable XGBoost

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --modelout MODEL_FILE
                        Output model file
  --dumpout DUMPOUT_PATH
                        Dump directory (directory to store metric values)
  --xgbparams XGB_PARAMS
                        Parameters of XGBoost constructor
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --trainds: percorso (relativo o assoluto) del file csv a due colonne (con header) che contiene il dataset da utilizzare per il training; questo file può essere generato in modo sintetico ad esempio tramite il programma fx_gen.py oppure essere un dataset ottenuto realmente misurando un fenomeno scalare e reale che dipende da una sola variabile reale.

  • --outputdim: il numero $n$ delle variabili indipendenti che devono corrispondere alle prime $n$ colonne del dataset csv; il resto delle colonne a destra sono considerante di conseguenza la $m$ variabili dipendenti.

  • --modelout: percorso (relativo o assoluto) al file dove salvare il modello addestrato nel formato joblib (.jl).

  • --dumpout: percorso (relativo o assoluto) della directory dove salvare i valori delle metriche allo scorrere delle epoche; il programma dumps_scatter.py utilizzerà il contenuto di questa directory per visualizzare i grafici delle metriche.

  • --xgbparams: lista di parametri da passare all'algoritmo di regressione di XGBoost; si veda la documentazione di XGBRegressor.

Predizione e calcolo dell'errore

In questo capitolo sono invece presentati i programmi predict_func_miso.py e predict_func_mimo.py il cui scopo è quello di effettuare le predizioni su un dataset di test applicandolo a un modello di regressore XGBoost addestrato precedentemente rispettivamente tramite il programma fit_func_miso.py e fit_func_mimo.py, sempre senza dover scrivere codice ma tramite la sola linea di comando.
Infatti questi due programmi supportano argomenti tramite i quali l'utente passa il modello addestrato precentemente, il dataset di test e le misure di errore da calcolare tra la predizione e il valore vero.
Il formato dei dataset di test in ingresso è rispettivamente identico a quello dei programmi fit_func_miso.py e fit_func_mimo.py; ovviamente le ultime colonne (relative alle variabili dipendenti) sono adoperate solo per confrontare i valori predetti con i valori veri con i valori veri calcolando le misure di errore passate.

Usage del programma predict_func_miso.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python predict_func_miso.py --help
e l'output ottenuto è: 

usage: predict_func_miso.py [-h] [--version] --model MODEL_FILE --ds
                            DF_PREDICTION --predictionout PREDICTION_DATA_FILE
                            [--measures MEASURES [MEASURES ...]]

predict_func_miso.py makes prediction of the values of a multiple-input
single-output (scalar) function with a pretrained XGBoost model

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --model MODEL_FILE    model file
  --ds DF_PREDICTION    dataset file (csv format)
  --predictionout PREDICTION_DATA_FILE
                        prediction data file (csv format)
  --measures MEASURES [MEASURES ...]
                        List of built-in sklearn regression metrics to compare
                        prediction with input dataset
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --model: percorso (relativo o assoluto) al file nel formato joblib (.jl) del modello generato da fit_func_miso.py.

  • --ds: percorso (relativo o assoluto) del file csv (con header) che contiene il dataset di input su cui calcolare la predizione.

  • --predictionout: percorso (relativo o assoluto) del file csv da generare che conterrà la predizione, ovverosia l'approssimazione della funzione applicata al dataset di input.

  • --measures: lista di misure da calcolare confrontando i valori veri del dataset di input e i valori predetti in uscita; la lista delle metriche supportate è definita in SciKit Learn Regression Metrics.

Usage del programma predict_func_mimo.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python predict_func_mimo.py --help
e l'output ottenuto è: 

usage: predict_func_mimo.py [-h] [--version] --model MODEL_FILE --ds
                            DF_PREDICTION --outputdim NUM_OF_DEPENDENT_COLUMNS
                            --predictionout PREDICTION_DATA_FILE
                            [--measures MEASURES [MEASURES ...]]

predict_func_mimo.py makes prediction of the values of a multiple-input
single-output (scalar) function with a pretrained XGBoost model

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --model MODEL_FILE    model file
  --ds DF_PREDICTION    dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --predictionout PREDICTION_DATA_FILE
                        prediction data file (csv format)
  --measures MEASURES [MEASURES ...]
                        List of built-in sklearn regression metrics to compare
                        prediction with input dataset
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --model: percorso (relativo o assoluto) al file nel formato joblib (.jl) del modello generato da fit_func_miso.py.

  • --ds: percorso (relativo o assoluto) del file csv (con header) che contiene il dataset di input su cui calcolare la predizione.

  • --outputdim: il numero $n$ delle variabili indipendenti che devono corrispondere alle prime $n$ colonne del dataset csv; il resto delle colonne a destra sono considerante di conseguenza la $m$ variabili dipendenti.

  • --predictionout: percorso (relativo o assoluto) del file csv da generare che conterrà la predizione, ovverosia l'approssimazione della funzione applicata al dataset di input.

  • --measures: lista di misure da calcolare confrontando i valori veri del dataset di input e i valori predetti in uscita; la lista delle metriche supportate è definita in SciKit Learn Regression Metrics.

Un esempio di uso di tutti i programmi

Si supponga di voler approssimare nell'intervallo $[-0.4,0.4]$ la seguente funzione $$f(x)=x sin \frac{1}{x}$$ Tenendo presente che np è l'alias della libreria NumPy, questa si traduce in sintassi lambda body Python così: 

x * np.sin(1 / x)
Per generare il dataset di training, si esegua quindi il seguente comando: 

$ python fx_gen.py \
  --dsout mytrain.csv \
  --funcx "x * np.sin(1 / x)" \
  --xbegin -0.4 \
  --xend 0.4 \
  --xstep 0.00031
mentre per generare il dataset di test, si esegua il seguente comando: 

$ python fx_gen.py \
  --dsout mytest.csv \
  --funcx "x * np.sin(1 / x)" \
  --xbegin -0.4 \
  --xend 0.4 \
  --xstep 0.00073
Si osservi che il passo di discretizzazione del dataset di test è più grande di quello di training e questo è normale in quanto l'addestramento, per essere accurato, deve essere eseguito su una maggiore quantità di dati. Inoltre si osservi che è opportuno che il passo di discretizzazione del dataset di test non sia un multiplo di quello di training per garantire che il dataset di test contenga la maggior parte dei dati non presenti nel dataset di training, e questo rende più interessante la predizione.

A questo si intende effettuare una regressione tramite fit_func_miso.py passando al regressore sottostante i seguenti argomenti: n_estimators: 100, max_depth: 7; quindi si esegua quindi il seguente comando: 

$ python fit_func_miso.py \
  --trainds mytrain.csv \
  --modelout mymodel.jl \
  --xgbparams "'n_estimators': 100, 'max_depth': 7"
e alla fine dell'esecuzione il file mymodel.jl salvato contiene il modello del regressore XGBoost configurato e addestrato.

Adesso si intende effettuare la predizione e il calcolo dell'errore usando le misure mean_absolute_error e mean_squared_error; quindi si esegua quindi il seguente comando: 

$ python predict_func_miso.py \
  --model mymodel.jl \
  --ds mytest.csv \
  --predictionout mypred.csv \
  --measures mean_absolute_error mean_squared_error
e alla fine dell'esecuzione il file mypred.csv salvato contiene la predizione eseguita applicando il modello sui dati di test; l'output del programma visualizza le misure di errore passate tramite l'argomento --measures e sono molto piccole: la prima intorno a $1.5 \cdot 10^{-3}$ e la seconda intorno a $5.5 \cdot 10^{-6}$
Nota: Data la natura stocastica della fase di addestramento, i singoli specifici risultati possono variare. Si consideri di eseguire la fase di addestramento più volte.

Infine si desidera intende effettuare la visualizzazione comparata del dataset di test con la predizione; si esegua perciò il seguente comando: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --title "XGBoost (estimators: 100, max depth: 7)" \
  --xlabel "x" \
  --ylabel "y=x sin(1/x)"
che mostra i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati, come del resto le basse misure dell'errore già indicavano; solamente intorno allo zero si osserva qualche imprecisione ed è dovuta all'oscillazione della funzione che è lì molto forte.

Nota: Data la natura stocastica della fase di addestramento, i singoli specifici risultati possono variare. Si consideri di eseguire la fase di addestramento più volte.

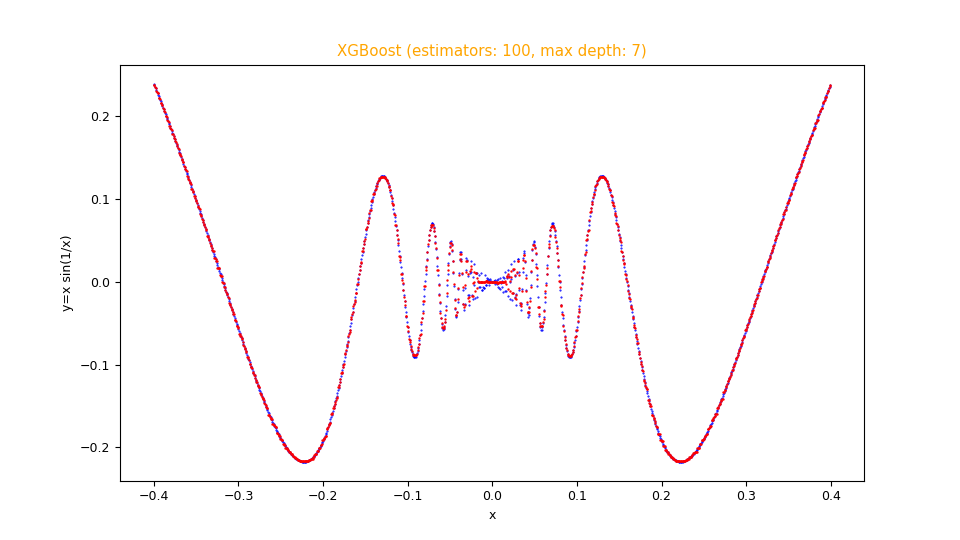
Figura con grafici a dispersione generata dal programma fx_scatter.py che mostra l'approssimazione in sovraimpressione in rosso della funzione $f(x)=x sin \frac{1}{x}$ e la funzione originale sottostante in blu.

Il repository contiene degli esempi in script shell che mostrano l'uso di questi programmi in cascata:


Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.