Approssimazione di funzioni tramite un Support Vector Regressor configurabile

Questo post tratta l'approssimazione di funzioni matematiche reali, sia scalari che vettoriali, a una o più variabili reali tramite il Support Vector Regressor senza scrivere codice ma agendo solo sulla linea di comando di script Python che implementano le funzionalità di:

  • Configurazione del regressore e addestramento
  • Predizione e calcolo dell'errore
Il codice descritto da questo post richiede la versione 3 di Python e utilizza la libreria SciKit-Learn; richiede inoltre le librerie NumPy, Pandas, MatPlotLib e JobLib. Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.

Per quanto riguarda la generazione dei dataset sintetici di training e di test si farà uso dei seguenti strumenti (presenti nel repository):
  • fx_gen.py per le funzioni generatrici scalari reali di una variabile reale $f(x) \colon [a,b] \to {\rm I\!R}$
  • fxy_gen.py per le funzioni generatrici scalari reali di due variabili reali $f(x,y) \colon [a,b] \times [c,d] \to {\rm I\!R}$
  • pcm2t_gen.py per le curve parametriche sul piano, quindi funzioni vettoriali reali $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R}$
  • pmc3t_gen.py per le curve parametriche nello spazio, quindi funzioni vettoriali reali $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R \times \rm I\!R}$
Per la visualizzazione dei risultati, e precisamente per la comparazione del dataset di test con la predizione, si farà uso dei seguenti strumenti (sempre presenti nel repository):

Configurazione del regressore e addestramento

In questo capitolo vengono presentati due programmi: fit_func_esvr.py e fit_func_nusvr.py che tecnicamente sono wrapper rispettivamente delle classi della libreria SciKit-Learn sklearn.svm.SVR e sklearn.svm.NuSVR che implementano gli algoritmi epsilon-Support-Vector-Regressor e nu-Support-Vector-Regressor e il fine dei due programmi è di consentire l'utilizzazione dei regressori sottostanti per approssimare funzioni senza dover scrivere codice ma agendo solo sulla linea di comando.
Infatti tramite l'argomento --svrparams l'utente passa una serie di iper parametri per regolare il comportamento dell'algoritmo SVR sottostante e altri per configurare l'apprendimento dello stesso. Oltre ai parametri del regressore sottostante i due programmi supportano dei propri argomenti per consentire all'utente di passare il dataset di training e il file ove salvare il modello addestrato.

Entrambi i programmi sono di tipo M.I.M.O., cioè Multiple Input Multiple Output: sono progettati per approssimare una funzione della forma $f \colon \rm I\!R^n \to \rm I\!R^m$ utilizzando nell'implementazione la classe sklearn.multioutput.MultiOutputRegressor.
Il formato dei dataset in ingresso è in formato csv (con header), con $n + m$ colonne, di cui le prime $n$ colonne contengono i valori delle $n$ variabili indipendenti e le ultime $m$ contenenti i valori delle variabili dipendenti.

Usage del programma fit_func_esvr.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python fit_func_esvr.py --help
e l'output ottenuto è: 

usage: fit_func_esvr.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                        --outputdim NUM_OF_DEPENDENT_COLUMNS --modelout
                        MODEL_FILE [--dumpout DUMPOUT_PATH]
                        [--svrparams SVR_PARAMS]

fit_func_esvr.py fits a multiple-input multiple-output function dataset using
a configurable Epsilon-Support Vector Regressor

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --modelout MODEL_FILE
                        Output model file
  --svrparams SVR_PARAMS
                        Parameters of Epsilon-Support Vector Regressor
                        constructor
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --trainds: percorso (relativo o assoluto) del file csv a $n+m$ colonne (con header) che contiene il dataset da utilizzare per il training; questo file può essere generato in modo sintetico ad esempio tramite uno dei programmi di cui sopra oppure essere un dataset del mondo reale che mappa $n$ variabili indipendenti su $m$ variabili dipendenti.

  • --outputdim: il numero $n$ delle variabili indipendenti che devono corrispondere alle prime $n$ colonne del dataset csv; il resto delle colonne a destra sono considerante di conseguenza la $m$ variabili dipendenti.

  • --modelout: percorso (relativo o assoluto) al file dove salvare il modello addestrato nel formato joblib (.jl).

  • --svrparams: lista di parametri da passare all'algoritmo di regressione sottostante; si veda la documentazione di sklearn.svm.SVR.

Usage del programma fit_func_nusvr.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python fit_func_nusvr.py --help
e l'output ottenuto è: 

usage: fit_func_nusvr.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                         --outputdim NUM_OF_DEPENDENT_COLUMNS --modelout
                         MODEL_FILE [--dumpout DUMPOUT_PATH]
                         [--svrparams SVR_PARAMS]

fit_func_nusvr.py fits a multiple-input multiple-output function dataset using
a configurable Nu-Support Vector Regressor

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --modelout MODEL_FILE
                        Output model file
  --svrparams SVR_PARAMS
                        Parameters of Nu-Support Vector Regressor constructor
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --trainds: percorso (relativo o assoluto) del file csv a $n$+$m$ colonne (con header) che contiene il dataset da utilizzare per il training; questo file può essere generato in modo sintetico ad esempio tramite uno dei programmi di cui sopra oppure essere un dataset del mondo reale che mappa $n$ variabili indipendenti su $m$ variabili dipendenti.

  • --outputdim: il numero $n$ delle variabili indipendenti che devono corrispondere alle prime $n$ colonne del dataset csv; il resto delle colonne a destra sono considerante di conseguenza la $m$ variabili dipendenti.

  • --modelout: percorso (relativo o assoluto) al file dove salvare il modello addestrato nel formato joblib (.jl).

  • --svrparams: lista di parametri da passare all'algoritmo di regressione sottostante; si veda la documentazione di sklearn.svm.NuSVR.

Predizione e calcolo dell'errore

In questo capitolo viene invece presentato il programma predict_func.py il cui scopo è quello di effettuare le predizioni su un dataset di test applicandolo a un modello e-SVR oppure nu-SVR addestrato precedentemente rispettivamente tramite il programma fit_func_esvr.py o fit_func_nusvr.py sempre senza dover scrivere codice ma tramite la sola linea di comando.
Infatti tale programma supporta argomenti tramite i quali l'utente passa il modello addestrato precentemente, il dataset di test e le misure di errore da calcolare tra la predizione e il valore vero.
Il formato dei dataset di test in ingresso è identico a quello dei programmi di training di cui sopra; ovviamente qui le ultime colonne (quelle delle variabili dipendenti) vengono adoperate solo per confrontare i valori predetti con i valori veri calcolando le misure di errore passate.

Usage del programma predict_func.py

Per ottenere l'usage del programma è sufficiente eseguire il seguente comando: 

$ python predict_func.py --help
e l'output ottenuto è: 

usage: predict_func.py [-h] [--version] --model MODEL_FILE --ds DF_PREDICTION
                       --outputdim NUM_OF_DEPENDENT_COLUMNS --predictionout
                       PREDICTION_DATA_FILE
                       [--measures MEASURES [MEASURES ...]]

predict_func.py makes prediction of the values of a multiple-input multiple-
output function with a pretrained Standard Vector Regressor model

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --model MODEL_FILE    model file
  --ds DF_PREDICTION    dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --predictionout PREDICTION_DATA_FILE
                        prediction data file (csv format)
  --measures MEASURES [MEASURES ...]
                        List of built-in sklearn regression metrics to compare
                        prediction with input dataset
Dove:
  • -h, --help: mostra l'usage del programma e termina l'esecuzione.

  • --version: mostra la versione del programma e termina l'esecuzione.

  • --model: percorso (relativo o assoluto) al file nel formato joblib (.jl) del modello generato da uno dei programmi di training sopra descritti.

  • --ds: percorso (relativo o assoluto) del file csv (con header) che contiene il dataset di input su cui calcolare la predizione.

  • --outputdim: il numero $n$ delle variabili indipendenti che devono corrispondere alle prime $n$ colonne del dataset csv; il resto delle colonne a destra sono considerante di conseguenza la $m$ variabili dipendenti.

  • --predictionout: percorso (relativo o assoluto) del file csv da generare che conterrà la predizione, ovverosia l'approssimazione della funzione applicata al dataset di input.

  • --measures: lista di misure da calcolare confrontando i valori veri del dataset di input e i valori predetti in uscita; la lista delle metriche supportate è definita in SciKit Learn Regression Metrics.

Un esempio di uso di tutti i programmi

Si supponga di voler approssimare nell'intervallo $[-0.10,10.0]$ la seguente funzione $$f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$$ Tenendo presente che np è l'alias della libreria NumPy, questa si traduce in sintassi lambda body Python così: 

0.5*x**3 - 2*x**2 - 3*x - 1
Per generare il dataset di training, si esegua quindi il seguente comando: 

$ python fx_gen.py \
  --dsout mytrain.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.01
mentre per generare il dataset di test, si esegua il seguente comando: 

$ python fx_gen.py \
  --dsout mytest.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.0475
Si osservi che il passo di discretizzazione del dataset di test è più grande di quello di training e questo è normale in quanto l'addestramento, per essere accurato, deve essere eseguito su una maggiore quantità di dati. Inoltre si osservi che è opportuno che il passo di discretizzazione del dataset di test non sia un multiplo di quello di training per garantire che il dataset di test contenga la maggior parte dei dati non presenti nel dataset di training, e questo rende più interessante la predizione.

A questo si intende effettuare una regressione tramite fit_func_esvr.py passando al regressore sottostante i seguenti argomenti: kernel: rbf, C: 100, gamma: 0.1, epsilon: 0.1; quindi si esegua quindi il seguente comando: 

$ python fit_func_esvr.py \
  --trainds mytrain.csv \
  --modelout mymodel.jl \
  --outputdim 1 \
  --svrparams "'kernel': 'rbf', 'C': 100, 'gamma': 0.1, 'epsilon': 0.1"
e alla fine dell'esecuzione il file mymodel.jl salvato contiene il modello del regressore e-svr configurato e addestrato.

Adesso si intende effettuare la predizione e il calcolo dell'errore usando le misure mean_absolute_error e mean_squared_error; quindi si esegua quindi il seguente comando: 

$ python predict_func.py \
  --model mymodel.jl \
  --ds mytest.csv \
  --outputdim 1 \
  --predictionout mypred.csv \
  --measures mean_absolute_error mean_squared_error
e alla fine dell'esecuzione il file mypred.csv salvato contiene la predizione eseguita applicando il modello sui dati di test; l'output del programma visualizza lo score molto molto vicino a 1 e le misure di errore passate tramite l'argomento --measures e sono accettabili: la prima intorno a $0.4$ e la seconda intorno a $1.9$
Nota: Data la natura stocastica della fase di addestramento, i singoli specifici risultati possono variare. Si consideri di eseguire la fase di addestramento più volte.

Infine si intende effettuare la visualizzazione comparata del dataset di test con la predizione; si esegua perciò il seguente comando: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --title "e-svr ('kernel': 'rbf', 'C': 100, 'gamma': 0.1, 'epsilon': 0.1)" \
  --xlabel "x" \
  --ylabel "y=1/2 x^3 - 2x^2 - 3x - 1"
che mostra i grafici a dispersione del dataset di test e la predizione sovrapposti: in blu quello del dataset di test, in rosso la predizione. La comparazione dei due grafici evidenzia chiaramente che l'approssimazione ha raggiunto livelli molto elevati.

Nota: Data la natura stocastica della fase di addestramento, i singoli specifici risultati possono variare. Si consideri di eseguire la fase di addestramento più volte.

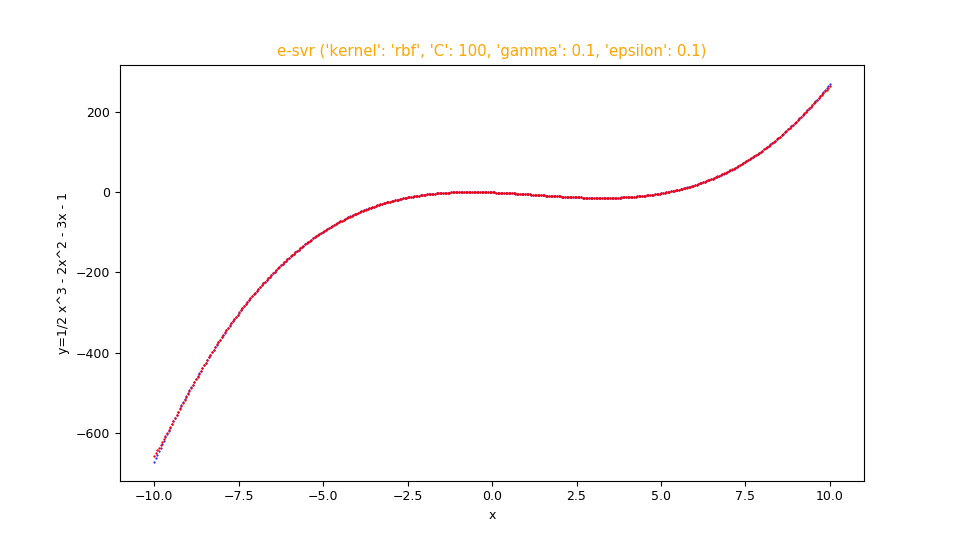
Figura con grafici a dispersione generata dal programma fx_scatter.py che mostra l'approssimazione in sovraimpressione in rosso della funzione $f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$ e la funzione originale sottostante in blu.

Se si intende invece effettuare una regressione tramite fit_func_nusvr.py passando al regressore sottostante i seguenti argomenti: C: 10, gamma: auto si esegua quindi il seguente comando: 

$ python fit_func_nusvr.py \
  --trainds mytrain.csv \
  --modelout mymodel.jl \
  --outputdim 1 \
  --svrparams "'C': 10, 'gamma': 'auto'"
quindi eseguire la predizione usando il comando predict_func.py con gli stessi parametri di sopra e infine per generare i grafici a dispersione eseguire il seguente comando: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --title "nu-svr ('C': 10, 'gamma': 'auto')" \
  --xlabel "x" \
  --ylabel "y=1/2 x^3 - 2x^2 - 3x - 1"
Il repository contiene degli esempi in script shell che mostrano l'uso di questi programmi in cascata:


Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.