Risoluzione di equazioni differenziali con ritardo con metodi numerici in Python

Le equazioni differenziali con ritardo sono adoperate nella modellazione matematica di sistemi ove le reazioni alle sollecitazioni avvengono non immediatamente ma dopo un certo lasso di tempo non trascurabile. Le equazioni differenziali con ritardo sono un campo ampio e complicato della matematica ancora oggi oggetto di ricerca; la risoluzione analitica di tali equazioni è, quando fattibile, certamente non banale: si veda il post su questo sito Un metodo di soluzione di una equazione differenziale con ritardo del primo ordine utilizzando la funzione W di Lambert per una trattazione sulla risoluzione analitica di una particolare classe di tali equazioni.
Questo post invece si occupa di tecniche di risoluzioni numeriche in Python utilizzando due diverse librerie: ddeint e JiTCDDE; ddeint è basata su Scipy mentre JiTCDDE produce codice C che viene compilato ed eseguito. Questo post non entra nel merito dell'implementazione di queste due librerie, ma si concentra sull'usage procedendo per esempi a complessità crescente.

Tutti i vari esempi di codice descritti in questo post richiedono la versione 3 di Python e le librerie NumPy e MatPlotLib; addizionalmente gli script basati su ddeint richiedono SciPy per quanto detto prima, mentre quelli basati su JiTCDDE richiedono SymPy.

Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.

Convenzioni

In questo post le convenzioni adoperate sono le seguenti:

• L'abbreviazione DDE indica una equazione differenziale con ritarto e sta per Delay Differential Equation.
• L'abbreviazione ODE indica una equazione differenziale ordinaria e sta per Ordinary Differential Equation.
• L'abbreviazione IVP indica un problema a valori iniziali, detto anche problema di Cauchy, e sta per Initial Value Problem.
• $t$ è la variabile indipendente, indica il tempo ed è espressa in secondi.
• $y$ è la funzione incognita, ed è da intendersi come funzione di t, ovverosia $y=y(t)$, ma l'uso di questa notazione compatta, oltre ad avere una maggiore leggibilità a livello matematico rende più agevole la "traduzione" in codice dell'equazione.
• $y_1$ e $y_2$ sono le funzioni incognite nel caso dei sistemi di due equazioni.
• L'istante $t=0$ è assunto come tempo iniziale, quindi negli esempi successivi sarà sempre $t_0=0$.
• $\phi$ indica la funzione storica iniziale, ovverosia la funzione che fornisce i valori della funzione incognita $y$ per valori di $t \leq t_0$.
  
• $\tau$ indica la funzione ritardo, è da intendersi come funzione di $t$ e di $y$, ovverosia $\tau=f(t, y(t))$.
  
• $y'$ è la derivata prima di $y$ rispetto a $t$.
• $y''$ è la derivata seconda di $y$ rispetto a $t$.

Osservazioni sulle condizioni iniziali delle DDE

Nel caso di una ODE in un IVP oltre all'equazione sono date tante condizioni iniziali in funzione dell'ordine dell'equazione e sono della forma: $y(t_0)=y_0$, $y'(t_0)=y'_0$, e così via (per un elenco completo delle altre condizioni per garantire l'esistenza e l'unicità della soluzione si veda il teorema di Picard-Lindelöf).
Per le DDE invece non basta dare un insieme di valori iniziali per la funzione e le sue derivate in $t_0$, ma bisogna dare un insieme di funzioni per fornire i valori storici per $t_0 - max(\tau) \leq t \leq t_0$.
Quanti e quali funzioni storiche dare per avere una soluzione unica dipende dall'ordine dell'equazione: per una equazione del primo ordine bisogna dare una sola $\phi$ per fornire i valori storici di $y$. Per una equazione del secondo ordine bisogna dare una $\phi$ per fornire i valori storici di $y$ e un'altra $\phi$ per fornire i valori storici di $y'$. Per un sistema di equazioni del primo ordine bisogna dare due $\phi$ per fornire i valori storici di $y_1$ e $y_2$. E così via.

Note tecniche

Seppur, come detto sopra, questo post non entra nel dettaglio dell'implementazione, è importante fornire qualche nota tecnica prima di procedere con gli esempi.

ddeint

ddeint è una libreria Python che contiene una omonima classe, che è il cuore dell'implementazione, il cui scopo è di sovrascrive alcune funzioni di scipy.integrate.ode per consentire l'aggiornamento di una pseudo-variabile (che rappresenza la funzione incognita) ad ogni passo di integrazione; la libreria è stata sviluppa da Zulko, il sorgente è disponibile all'indirizzo: https://github.com/Zulko/ddeint e la libreria è installabile con il seguente comando:

$ pip install ddeint

Note sintattiche

Nel codice, la definizione della DDE (o del sistema di DDE) è una funzione Python con almeno due argomenti:

• il primo argomento è l'incognita (generamente con nome Y);
• il secondo argomento è il tempo (generalmente con nome t).

def equation(Y, t):
    return -Y(t - 1)

def equations(Y, t, d):
    x,y = Y(t)
    xd,yd = Y(t-d)
    return [x * yd, y * xd]

JiTCDDE

JiTCDDE sta per compilazione just-in-time di DDE; prende un iterabile di espressioni SymPy, le traduce in codice C, le compila al volo e invoca il codice compilato da Python; la libreria è stata sviluppa da Neurophysik, il sorgente è disponibile all'indirizzo: https://github.com/neurophysik/jitcddet e la libreria è installabile con il seguente comando:

$ pip install jitcdde

Note sintattiche

Nel codice, la definizione della DDE (o del sistema di DDE) è una lista Python; per ogni elemento della lista valgono queste regole:

• il nome y è l'incognita; è un nome simbolico SymPy importato da jitcdde; y a sua volta è una funzione Python ove il primo argomento è l'indice delle componenti dell'incognita stessa mentre il secondo argomento è il tempo t;
• il nome t è il tempo; anche questo è un nome simbolico SymPy importato da jitcdde

equation = [-y(0, t-1.)]

d=symengine.symbols("d")
equations=[
	y(0, t) * y(1, t-d),
	y(1, t) * y(0, t-d)]

Esempio #1: DDE del primo ordine a ritardo costante e funzione storica iniziale costante

Sia data la seguente DDE: $$ y'(t)=-y(t-1) $$ ove il ritardo è di $1 s$; l'esempio confronta le soluzioni di tre casi diversi usando tre differenti funzioni storiche costanti:

• Caso #1: $\phi(t)=-1$
• Caso #2: $\phi(t)=0$
• Caso #3: $\phi(t)=1$

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def equation(Y, t):
    return -Y(t - 1)

def initial_history_func_m1(t):
    return -1.

def initial_history_func_0(t):
    return 0.

def initial_history_func_p1(t):
    return 1.

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(3, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-1)$ solved by ddeint")

ts = np.linspace(0, 20, 2000)

ys = ddeint(equation, initial_history_func_m1, ts)
axs[0].plot(ts, ys, color='red', linewidth=1)
axs[0].set_title('$ihf(t)=-1$')

ys = ddeint(equation, initial_history_func_0, ts)
axs[1].plot(ts, ys, color='red', linewidth=1)
axs[1].set_title('$ihf(t)=0$')

ys = ddeint(equation, initial_history_func_p1, ts)
axs[2].plot(ts, ys, color='red', linewidth=1)
axs[2].set_title('$ihf(t)=1$')

plt.show()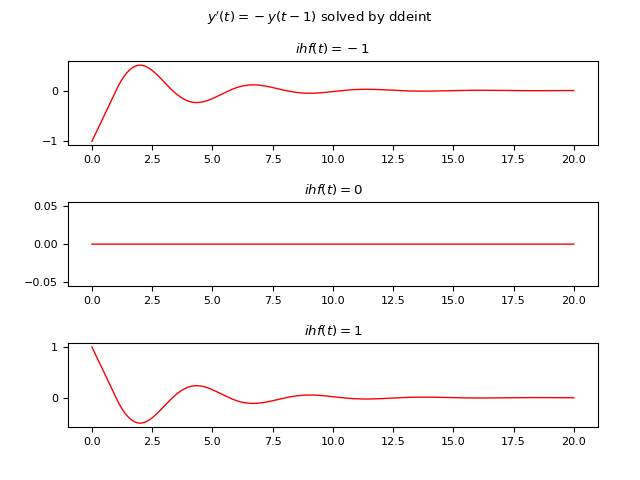

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

equation = [-y(0, t-1.)]
dde = jitcdde(equation)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(3, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-1)$ solved by jitcdde")

ts = np.linspace(0, 20, 2000)

dde.constant_past([-1.])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[0].plot(ts, ys, color='red', linewidth=1)
axs[0].set_title('$ihf(t)=-1$')

dde.constant_past([0])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[1].plot(ts, ys, color='red', linewidth=1)
axs[1].set_title('$ihf(t)=0$')

dde.constant_past([1.])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[2].plot(ts, ys, color='red', linewidth=1)
axs[2].set_title('$ihf(t)=1$')

plt.show()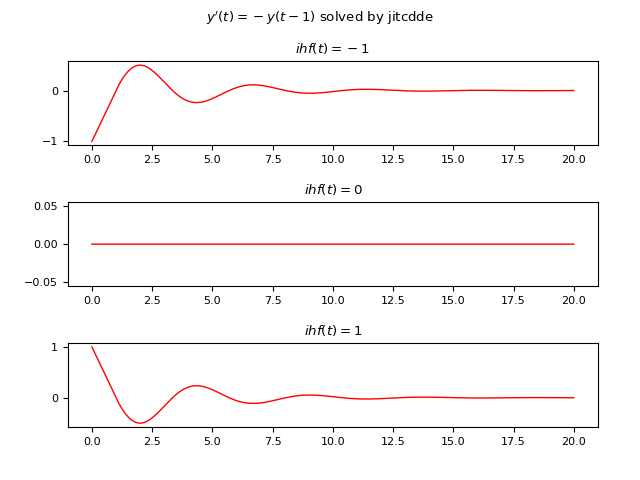

Esempio #2: DDE del primo ordine a ritardo costante e funzione storica iniziale non costante

Sia data la seguente DDE: $$ y'(t)=-y(t-2) $$ ove il ritardo è di $2 s$; l'esempio confronta le soluzioni di quattro casi diversi usando due differenti funzioni storiche (non costanti) e due diversi intervalli di $t$:

• Caso #1: $\phi(t)=e^{-t} - 1, t \in [0, 4]$
• Caso #2: $\phi(t)=e^{t} - 1, t \in [0, 4]$
• Caso #3: $\phi(t)=e^{-t} - 1, t \in [0, 60]$
• Caso #4: $\phi(t)=e^{t} - 1, t \in [0, 60]$

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def equation(Y, t):
    return -Y(t - 2)

def initial_history_func_exp_mt(t):
    return np.exp(-t) - 1

def initial_history_func_exp_pt(t):
    return np.exp(t) - 1

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(2, 2)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-2)$ solved by ddeint")

ts = np.linspace(0, 4, 2000)

ys = ddeint(equation, initial_history_func_exp_mt, ts)
axs[0, 0].plot(ts, ys, color='red', linewidth=1)
axs[0, 0].set_title('$ihf(t)=e^-t - 1, t \in [0, 4]$')

ys = ddeint(equation, initial_history_func_exp_pt, ts)
axs[0, 1].plot(ts, ys, color='red', linewidth=1)
axs[0, 1].set_title('$ihf(t)=e^t - 1, t \in [0, 4]$')

ts = np.linspace(0, 60, 2000)

ys = ddeint(equation, initial_history_func_exp_mt, ts)
axs[1, 0].plot(ts, ys, color='red', linewidth=1)
axs[1, 0].set_title('$ihf(t)=e^-t - 1, t \in [0, 60]$')

ys = ddeint(equation, initial_history_func_exp_pt, ts)
axs[1, 1].plot(ts, ys, color='red', linewidth=1)
axs[1, 1].set_title('$ihf(t)=e^t - 1, t \in [0, 60]$')

plt.show()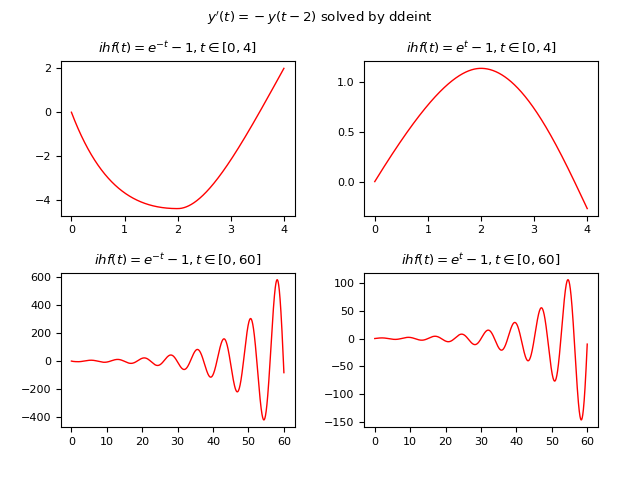

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

equation= [-y(0, t-2.)]
dde = jitcdde(equation)

def initial_history_func_exp_mt(t):
    return [np.exp(-t) - 1]

def initial_history_func_exp_pt(t):
    return [np.exp(t) - 1]

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(2, 2)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-2)$ solved by jitcdde")

ts = np.linspace(0, 4, 2000)

dde.past_from_function(initial_history_func_exp_mt)
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[0, 0].plot(ts, ys, color='red', linewidth=1)
axs[0, 0].set_title('$ihf(t)=e^-t - 1, t \in [0, 4]$')

dde.past_from_function(initial_history_func_exp_pt)
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[0, 1].plot(ts, ys, color='red', linewidth=1)
axs[0, 1].set_title('$ihf(t)=e^t - 1, t \in [0, 4]$')

ts = np.linspace(0, 60, 2000)

dde.past_from_function(initial_history_func_exp_mt)
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[1, 0].plot(ts, ys, color='red', linewidth=1)
axs[1, 0].set_title('$ihf(t)=e^-t - 1, t \in [0, 60]$')

dde.past_from_function(initial_history_func_exp_mt)
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[1, 1].plot(ts, ys, color='red', linewidth=1)
axs[1, 1].set_title('$ihf(t)=e^t - 1, t \in [0, 60]$')

plt.show()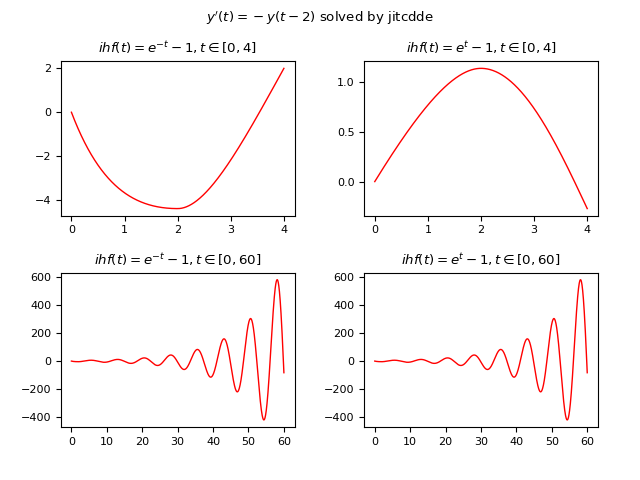

Esempio #3: DDE del primo ordine a ritardo non costante e funzione storica iniziale costante

Sia data la seguente DDE: $$ y'(t)=y(t-delay(y, t))$$ ove il ritardo non è costante ed è dato dalla funzione $delay(y, t)=|\frac{1}{10} t y(\frac{1}{10} t)|$; l'esempio confronta le soluzioni di due casi diversi usando due differenti funzioni storiche costanti:

• Caso #1: $\phi(t)=-1$
• Caso #2: $\phi(t)=1$

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def delay(Y, t):
    return np.abs(0.1 * t * Y(0.1 * t))

def equation(Y, t):
    return Y(t - delay(Y, t))

def initial_history_func_m1(t):
    return -1.

def initial_history_func_p1(t):
    return 1.

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(2, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=y(t-delay(y, t))$ solved by ddeint")

ts = np.linspace(0, 50, 10000)

ys = ddeint(equation, initial_history_func_m1, ts)
axs[0].plot(ts, ys, color='red', linewidth=1)
axs[0].set_title('$ihf(t)=-1$')

ys = ddeint(equation, initial_history_func_p1, ts)
axs[1].plot(ts, ys, color='red', linewidth=1)
axs[1].set_title('$ihf(t)=1$')

plt.show()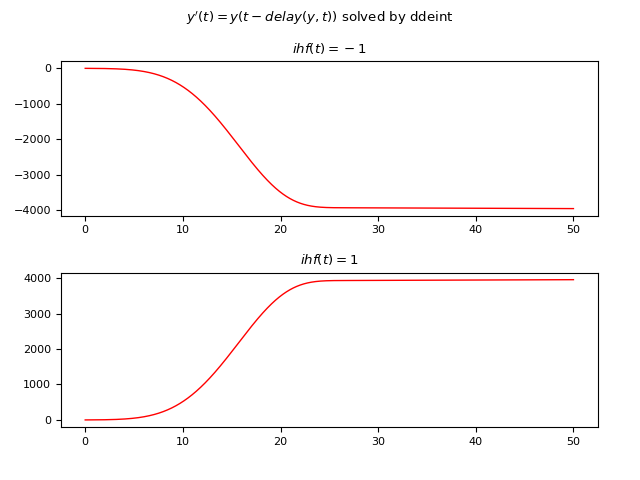

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

def delay(y, t):
    return np.abs(0.1 * t * y(0, 0.1 * t))

equation = [y(0, t - delay(y, t))]
dde = jitcdde(equation, max_delay=1000)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(2, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=y(t-delay(y, t))$ solved by jitcdde")

ts = np.linspace(0, 50, 10000)

dde.constant_past([-1.])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[0].plot(ts, ys, color='red', linewidth=1)
axs[0].set_title('$ihf(t)=-1$')

dde.constant_past([1.])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs[1].plot(ts, ys, color='red', linewidth=1)
axs[1].set_title('$ihf(t)=1$')

plt.show()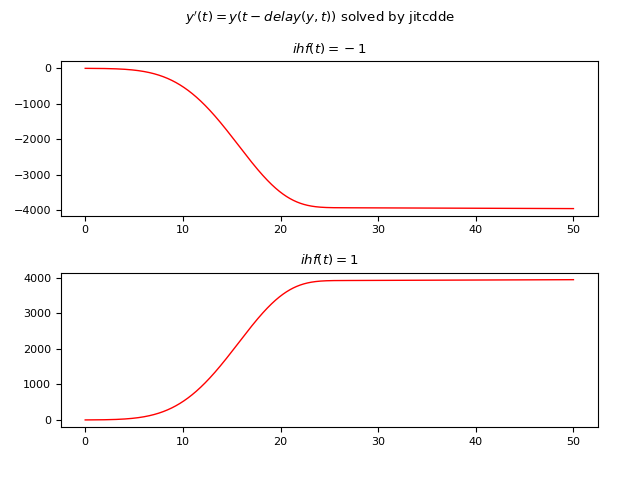

Esempio #4: DDE del primo ordine a ritardo non costante e funzione storica iniziale non costante

Sia data la seguente DDE: $$ y'(t)=y(t-delay(y, t))$$ ove il ritardo non è costante ed è dato dalla funzione $delay(y, t)=|\frac{1}{10} t y(\frac{1}{10} t)|$ e la funzione storica iniziale non è constante ed è $\phi(t)=e^t$.

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def delay(Y, t):
    return np.abs(0.1 * t * Y(0.1 * t))

def equation(Y, t):
    return Y(t - delay(Y, t))

def initial_history_func_exp_pt(t):
    return np.exp(t)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=y(t-delay(y, t))$ solved by ddeint")

ts = np.linspace(0, 30, 10000)

ys = ddeint(equation, initial_history_func_exp_pt, ts)
axs.plot(ts, ys, color='red', linewidth=1)
axs.set_title('$ihf(t)=e^t$')

plt.show()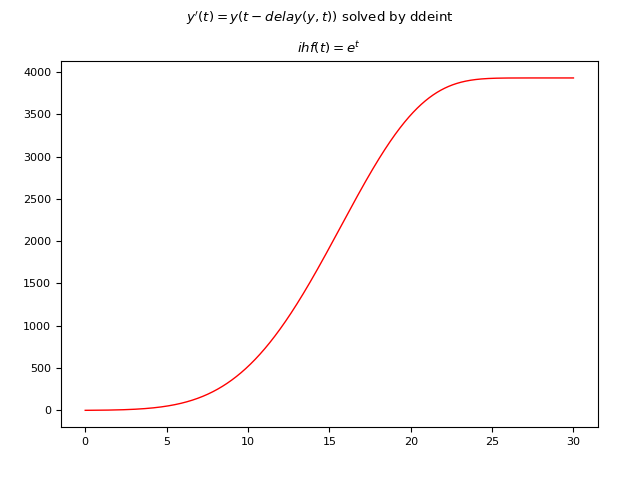

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

def delay(y, t):
    return np.abs(0.1 * t * y(0, 0.1 * t))

equation = [y(0, t - delay(y, t))]
dde = jitcdde(equation, max_delay=1000)

def initial_history_func_exp_pt(t):
    return [np.exp(t)]

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=y(t-delay(y, t))$ solved by jitcdde")

ts = np.linspace(0, 30, 10000)

dde.past_from_function(initial_history_func_exp_pt)
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs.plot(ts, ys, color='red', linewidth=1)
axs.set_title('$ihf(t)=e^t$')

plt.show()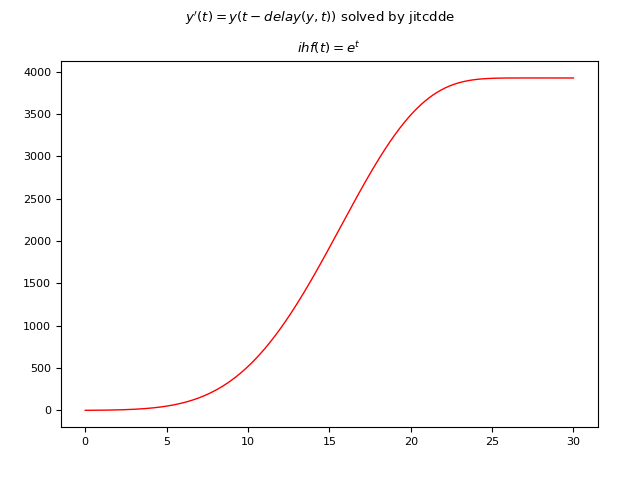

Esempio #5: DDE del primo ordine con due ritardi costanti e funzione storica iniziale costante

Sia data la seguente DDE: $$ y'(t)=-y(t - 1) + 0.3 y(t - 2)$$ ove i ritardi sono due e sono entrambi costanti pari rispettivamente a $1 s$ e $2 s$; anche la funzione storica iniziale è constante ed è $\phi(t)=1$.

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def equation(Y, t):
    return -Y(t - 1) + 0.3 * Y(t - 2)

def initial_history_func(t):
    return 1.

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-1) + 0.3\ y(t-2)$ solved by ddeint")

ts = np.linspace(0, 10, 10000)

ys = ddeint(equation, initial_history_func, ts)
axs.plot(ts, ys, color='red', linewidth=1)
axs.set_title('$ihf(t)=1$')

plt.show()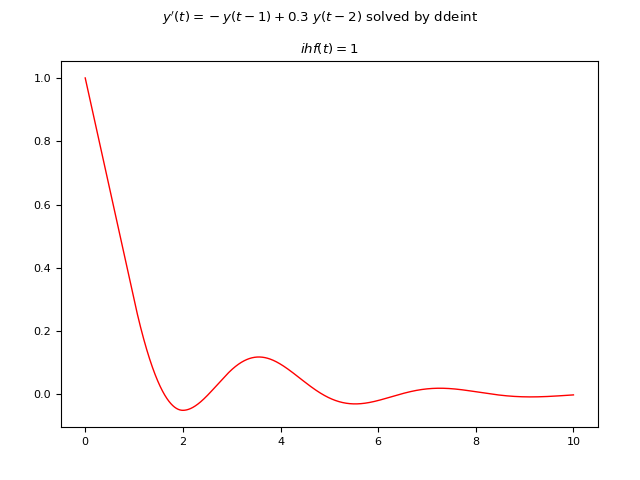

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

equation=[-y(0, t - 1) + 0.3 * y(0, t - 2)]
dde = jitcdde(equation)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y'(t)=-y(t-1) + 0.3\ y(t-2)$ solved by jitcdde")

ts = np.linspace(0, 10, 10000)

dde.constant_past([1.])
ys = []
for t in ts:
	ys.append(dde.integrate(t))
axs.plot(ts, ys, color='red', linewidth=1)
axs.set_title('$ihf(t)=1$')

plt.show()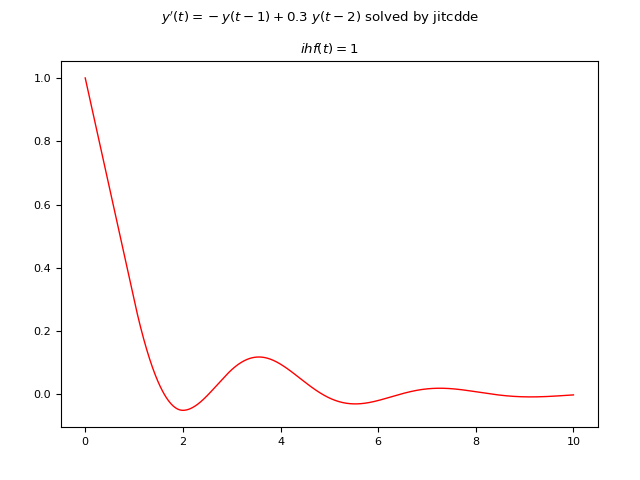

Esempio #6: Sistema di due DDE del primo ordine con un ritardo costante e due funzioni storiche iniziali costante

Sia dato il seguente sistema di DDE: $$ \begin{equation} \begin{cases} y_1'(t) = y_1(t) y_2(t-0.5) \\ y_2'(t) = y_2(t) y_1(t-0.5) \end{cases} \end{equation} $$ ove il ritardo è soltanto uno, costante e pari a $0.5 s$ e anche le funzioni storiche iniziali sono costanti; per quanto detto all'inizio del post queste devono essere due, infatti essendo l'ordine del sistema di primo grado ne serve una per ogni incognita e sono: $y_1(t)=1, y_2(t)=-1$.

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def equation(Y, t, d):
    x,y = Y(t)
    xd,yd = Y(t-d)
    return [x * yd, y * xd]

def initial_history_func(t):
    return [1., -1.]

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$x'(t)=x(t) y(t-d); y'(t)=y(t) x(t-d)$ solved by ddeint")

ts = np.linspace(0, 3, 2000)

ys = ddeint(equation, initial_history_func, ts, fargs=(0.5,))
axs.plot(ts, ys[:,0], color='red', linewidth=1)
axs.plot(ts, ys[:,1], color='blue', linewidth=1)
axs.set_title('$ihf_x(t)=1; ihf_y(t)=-1; d=0.5$')

plt.show()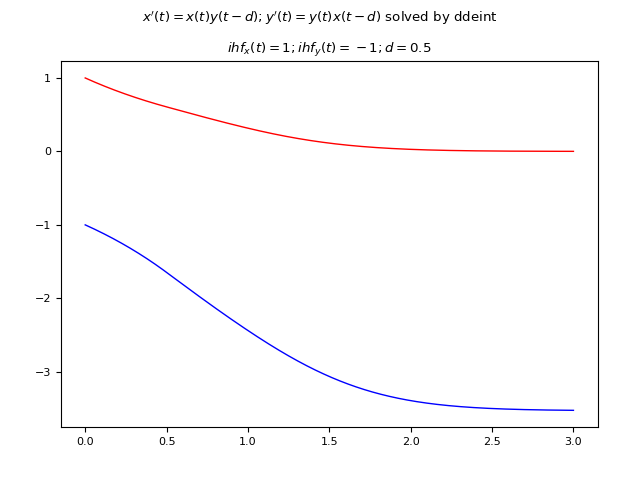

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
import symengine
from jitcdde import jitcdde, y, t

d=symengine.symbols("d")
equations=[
	y(0, t) * y(1, t-d),
	y(1, t) * y(0, t-d)]
ddesys = jitcdde(equations, control_pars=[d], max_delay=100.)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$x'(t)=x(t) y(t-d); y'(t)=y(t) x(t-d)$ solved by jitcdde")

ts = np.linspace(0, 3, 2000)

ddesys.constant_past([1., -1.])
params=[0.5]
ddesys.set_parameters(*params)
ys = []
for t in ts:
	ys.append(ddesys.integrate(t))
ys=np.array(ys)
axs.plot(ts, ys[:,0], color='red', linewidth=1)
axs.plot(ts, ys[:,1], color='blue', linewidth=1)
axs.set_title('$ihf_x(t)=1; ihf_y(t)=-1; d=0.5$')

plt.show()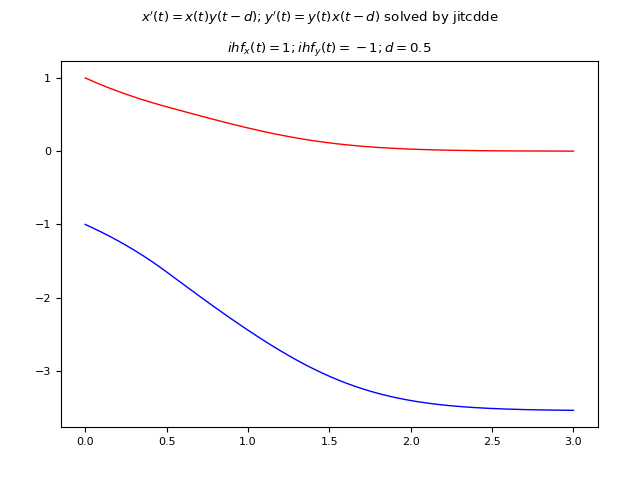

Esempio #7: DDE del secondo ordine con un ritardo costante e due funzione storiche iniziali costante

Sia data la seguente DDE: $$ y(t)'' = -y'(t) - 2y(t) - 0.5 y(t-1) $$ ove il ritardo è soltanto uno, costante e uguale a $1 s$. Poiché la DDE è del secondo ordine, in quanto compare la derivata seconda della funzione incognita, le funzioni storiche devono essere due, una per fornire i valori dell'incognita $y(t)$ per $t <= 0$ e una e una per fornire il valore della derivata prima $y'(t)$ sempre per $t <= 0$.
In questo esempio esse sono le seguenti due funzioni costanti: $y(t)=1, y'(t)=0$.
Per le proprità delle equazioni del secondo ordine, la DDE data equivale al seguente sistema di equazioni del primo ordine: $$ \begin{equation} \begin{cases} y_1'(t) = y_2(t) \\ y_2'(t) = -y_1'(t) - 2y_1(t) - 0.5 y_1(t-1) \end{cases} \end{equation} $$ e quindi l'implementazione rientra nella casistica del precedente esempio dei sistemi di equazioni del primo ordine.

ddeint

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando ddeint:

import numpy as np
import matplotlib.pyplot as plt
from ddeint import ddeint

def equation(Y, t):
    y,dydt = Y(t)
    ydelay, dydt_delay = Y(t-1)
    return [dydt, -dydt - 2 * y - 0.5 * ydelay]

def initial_history_func(t):
    return [1., 0.]

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y''(t)=-y'(t) - 2 y(t) - 0.5 y(t-1)$ solved by ddeint")

ts = np.linspace(0, 16, 4000)

ys = ddeint(equation, initial_history_func, ts)
axs.plot(ts, ys[:,0], color='red', linewidth=1)
#axs.plot(ts, ys[:,1], color='green', linewidth=1)
axs.set_title('$ihf_y(t)=1; ihf_dy/dt(t)=0$')

plt.show()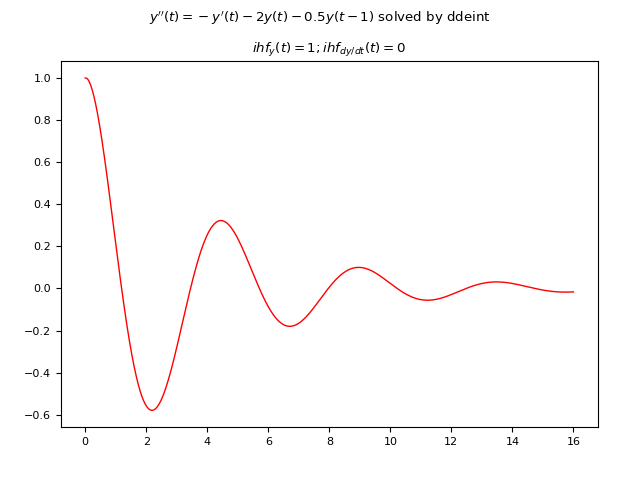

JiTCDDE

Qui di seguito un esempio di codice Python che risolve numericamente la DDE usando JiTCDDE:

import numpy as np
import matplotlib.pyplot as plt
from jitcdde import jitcdde, y, t

equations=[
    y(1, t),
    -y(1, t) - 2 * y(0, t) - 0.5 * y(0, t-1)
]
ddesys = jitcdde(equations)

plt.rcParams['font.size'] = 8
fig, axs = plt.subplots(1, 1)
fig.tight_layout(rect=[0, 0, 1, 0.95], pad=3.0)
fig.suptitle("$y''(t)=-y'(t) - 2 y(t) - 0.5 y(t-1)$ solved by jitcdde")

ts = np.linspace(0, 16, 4000)

ddesys.constant_past([1., 0.])
ys = []
for t in ts:
	ys.append(ddesys.integrate(t))
ys=np.array(ys)
axs.plot(ts, ys[:,0], color='red', linewidth=1)
#axs.plot(ts, ys[:,1], color='green', linewidth=1)
axs.set_title('$ihf_y(t)=1; ihf_dy/dt(t)=0$')

plt.show()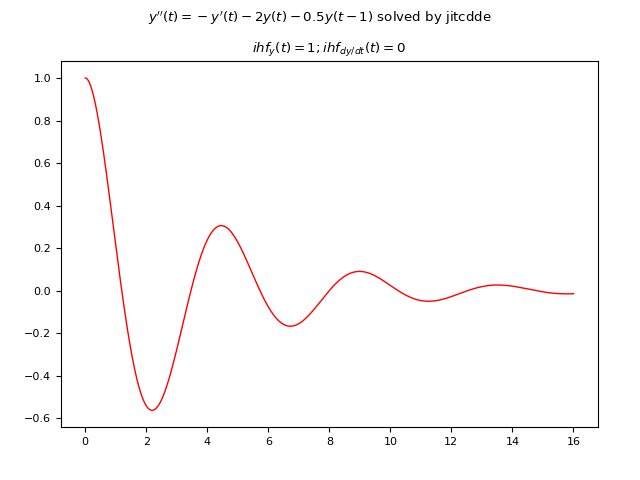

Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.