Esperimenti con Neural ODEs in Python con TensorFlowDiffEq

Neural Ordinary Differential Equations (abbreviato Neural ODEs) è un paper che introduce una nuova famiglia di reti neurali in cui alcuni strati nascosti (o anche l'unico strato nei casi più semplici) sono implementati con un risolutore di equazioni differenziali ordinarie.
Questo post mostra un esempio scritto in Python con TensorFlowDiffEq (in futuro ce ne saranno altri) che utilizza alcune idee descritte nel paper Neural ODEs per risolvere un problema di approssimazione della mappatura tra un input e un output in uno preciso scenario.

Tutti i vari frammenti di codice descritti in questo post richiedono la versione 3.x di Python, TensorFlow 2.x, il package TensorFlowDiffEq e i seguenti package: NumPy, MatPlotLib.
Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.
Se si fosse interessati a vedere la soluzione degli stessi problemi in Julia si veda il post Esperimenti con Neural ODEs in Julia su questo sito web.

Convenzioni

In questo post le convenzioni adoperate sono le seguenti:

  • $t$ è la variabile indipendente
  • $x$ è la funzione incognita
  • $y$ è la seconda funzione incognita
  • $x$ e $y$ sono da intendersi funzioni di $t$, quindi $x=x(t)$ e $y=y(t)$, ma l'uso di questa notazione compatta, oltre ad avere una maggiore leggibilità a livello matematico rende più agevole la "traduzione" in codice dell'equazione
  • $x'$ è la derivata prima di x rispetto a $t$ e naturalmente $y'$ è la derivata prima di y rispetto a $t$


Esperimento #1: addestrare un sistema di ODE per soddisfare un obiettivo

Un percettrone multistrato (abbreviato MLP) è uno strumento opportuno per imparare una relazione non lineare tra input e output di cui non si conosce la legge.
Ci sono casi invece in cui si ha conoscenza a priori della legge che correla gli input e gli output, ad esempio nella forma di un sistema parametrico di equazioni differenziali: in questa situazione una rete neurale di tipo MLP non consente di utilizzare tale conoscenza mentre una rete di tipo Neural ODEs sì.

Lo scenario di applicazione

Lo scenario di applicazione è il seguente:

    Conoscenza a priori:
    • Un dataset che contenga gli input e gli output
    • Una legge che associ input e output in forma di sistema parametrico di equazioni differenziali
    Obiettivo:
    • Determinare opportuni valori dei parametri affiché il sistema ottenuto sostituendo i parametri formali con i valori determinati approssimi al meglio la mappatura tra input e output.
    Lo stesso scenario è stato applicato nel repository neural-ode di mandubian su GitHub ove la legge è il sistema di equazioni di Lotka-Volterra che descrive la dinamica della popolazione di prede e predatori.
    In questo post la legge non è volutamente una legge famosa, ma è il sistema parametrico di due equazioni del primo ordine e otto parametri mostrato nel seguente paragrafo.

    Il problema da risolvere

    Sia dato il seguente sistema parametrico di due equazioni differenziali ordinarie con valori iniziali che rappresenta la legge che descrive il comportamento di un ipotetico sistema dinamico: $$ \begin{equation} \begin{cases} x' = a_1x + b_1y + c_1e^{-d_1t} \\ y'= a_2x + b_2y + c_2e^{-d_2t} \\ x(0)=0 \\ y(0)=0 \end{cases} \end{equation} $$ Ovviamente questa è una demo il cui scopo è provare la bontà del metodo, quindi per preparare il dataset fissiamo arbitrariamente gli otto valori dei parametri, ad esempio questi: $$ \left[\begin{matrix}a_1 \\ b_1 \\ c_1 \\ d_1 \\ a_2 \\ b_2 \\ c_2 \\ d_2 \end{matrix} \right] = \left[\begin{matrix}1.11 \\ 2.43 \\ -3.66 \\ 1.37 \\ 2.89 \\ -1.97 \\ 4.58 \\ 2.86 \end{matrix} \right] $$ e sapendo che con tali valori dei parametri la soluzione analitica è la seguente: $$ \begin{equation} \begin{array}{l} x(t) = \\ \;\; -1.38778 \cdot 10^{-17} \; e^{-8.99002 t} - \\ \;\; 2.77556 \cdot 10^{-17} \; e^{-7.50002 t} + \\ \;\; 3.28757 \; e^{-3.49501 t} - \\ \;\; 3.18949 \; e^{-2.86 t} + \\ \;\; 0.258028 \; e^{-1.37 t} - \\ \;\; 0.356108 \; e^{2.63501 t} + \\ \;\; 4.44089 \cdot 10^{-16} \; e^{3.27002 t} + \\ \;\; 1.11022 \cdot 10^{-16} \; e^{4.76002 t} \\ \\ y(t) = \\ \;\; -6.23016 \; e^{-3.49501 t} + \\ \;\; 5.21081 \; e^{-2.86 t} + \\ \;\; 1.24284 \; e^{-1.37 t} - \\ \;\; 0.223485 \; e^{2.63501 t} + \\ \;\; 2.77556 \cdot 10^{-17} \; e^{4.76002 t} \\ \end{array} \end{equation} $$ (verificabile online tramite Wolfram Alpha) si è in grado di preparare il dataset: l'input è un intervallo discretizzato del tempo da $0$ a $1.5$ passo $0.01$, mentre l'output è costituito dalle soluzioni analitiche $x=x(t)$ e $y=y(t)$ per ogni $t$ appartenente all'input.
    Una volta preparato il dataset ci si dimentichi dei valori dei parametri e della soluzione analitica e ci si pone il problema di come addestrare una rete neurale per determinare un opportuno set di valori per gli otto parametri per approssimare al meglio la mappatura non lineare tra input e output del dataset.

    L'implementazione della soluzione

    Il sistema parametrico di equazioni differenziali è già scritto in forma esplicita e in Python con TensorFlowDiffEq si implementa così: 

    def parametric_ode_system(t, u, args):
    a1, b1, c1, d1, a2, b2, c2, d2 = \
        args[0], args[1], args[2], args[3], \
        args[4], args[5], args[6], args[7]
    x, y = u[0], u[1]
    dx_dt = a1*x + b1*y + c1*tf.math.exp(-d1*t)
    dy_dt = a2*x + b2*y + c2*tf.math.exp(-d2*t)
    return tf.stack([dx_dt, dy_dt])
    I setting sono:
    • Input: $t \in [0, 1.5]$ passo di discretizzazione $0.01$
    • Condizioni al contorno: $x(0)=0; y(0)=0$
    • Valori iniziali del parametri qualsiasi; per comodità qui si impostano tutti uguali a $1$
    In codice:

    t_begin=0.
t_end=1.5
t_nsamples=150
t_space = np.linspace(t_begin, t_end, t_nsamples)
t_space_tensor = tf.constant(t_space)
x_init = tf.constant([0.], dtype=t_space_tensor.dtype)
y_init = tf.constant([0.], dtype=t_space_tensor.dtype)
u_init = tf.convert_to_tensor([x_init, y_init], dtype=t_space_tensor.dtype)
args = [tf.Variable(initial_value=1., name='p' + str(i+1), trainable=True,
          dtype=t_space_tensor.dtype) for i in range(0, 8)]
    La rete neurale è costituita da un solo strato di tipo ODE solver:

    def net():
  return odeint(lambda ts, u0: parametric_ode_system(ts, u0, args),
                  u_init, t_space_tensor)

    Le impostazioni dell'addrestramento sono:
    • Ottimizzatore: Adam
    • Learning rate: $0.05$
    • Numero di epoche: $200$
    • Funzione di loss: somma dei quadrati delle differenze
    In codice:

    learning_rate = 0.05
epochs = 200
optimizer = tfko.Adam(learning_rate=learning_rate)

def loss_func(num_sol):
  return tf.reduce_sum(tf.square(dataset_outs[0] - num_sol[:, 0])) + \
         tf.reduce_sum(tf.square(dataset_outs[1] - num_sol[:, 1]))  

for epoch in range(epochs):
  with tf.GradientTape() as tape:
    num_sol = net()
    loss_value = loss_func(num_sol)
  print("Epoch:", epoch, " loss:", loss_value.numpy())
  grads = tape.gradient(loss_value, args)
  optimizer.apply_gradients(zip(grads, args))

    Qui di seguito il codice completo:

    import numpy as np
import matplotlib.pyplot as plt

import tensorflow as tf
import tensorflow.keras.optimizers as tfko
from tfdiffeq import odeint

def parametric_ode_system(t, u, args):
    a1, b1, c1, d1, a2, b2, c2, d2 = \
        args[0], args[1], args[2], args[3], \
        args[4], args[5], args[6], args[7]
    x, y = u[0], u[1]
    dx_dt = a1*x + b1*y + c1*tf.math.exp(-d1*t)
    dy_dt = a2*x + b2*y + c2*tf.math.exp(-d2*t)
    return tf.stack([dx_dt, dy_dt])

true_params = [1.11, 2.43, -3.66, 1.37, 2.89, -1.97, 4.58, 2.86]

an_sol_x = lambda t : \
  -1.38778e-17 * np.exp(-8.99002 * t) - \
  2.77556e-17 * np.exp(-7.50002 * t) + \
  3.28757 * np.exp(-3.49501 * t) - \
  3.18949 * np.exp(-2.86 * t) + \
  0.258028 * np.exp(-1.37 * t) - \
  0.356108 * np.exp(2.63501 * t) +  \
  4.44089e-16 * np.exp(3.27002 * t) + \
  1.11022e-16 * np.exp(4.76002 * t)

an_sol_y = lambda t : \
  -6.23016 * np.exp(-3.49501 * t) + \
  5.21081 * np.exp(-2.86 * t) + \
  1.24284 * np.exp(-1.37 * t) - \
  0.223485 * np.exp(2.63501 * t) + \
  2.77556e-17 * np.exp(4.76002 * t)

t_begin=0.
t_end=1.5
t_nsamples=150
t_space = np.linspace(t_begin, t_end, t_nsamples)

dataset_outs = [tf.expand_dims(an_sol_x(t_space), axis=1), \
                tf.expand_dims(an_sol_y(t_space), axis=1)]

t_space_tensor = tf.constant(t_space)
x_init = tf.constant([0.], dtype=t_space_tensor.dtype)
y_init = tf.constant([0.], dtype=t_space_tensor.dtype)
u_init = tf.convert_to_tensor([x_init, y_init], dtype=t_space_tensor.dtype)
args = [tf.Variable(initial_value=1., name='p' + str(i+1), trainable=True,
          dtype=t_space_tensor.dtype) for i in range(0, 8)]

learning_rate = 0.05
epochs = 200
optimizer = tfko.Adam(learning_rate=learning_rate)

def net():
  return odeint(lambda ts, u0: parametric_ode_system(ts, u0, args),
                  u_init, t_space_tensor)

def loss_func(num_sol):
  return tf.reduce_sum(tf.square(dataset_outs[0] - num_sol[:, 0])) + \
         tf.reduce_sum(tf.square(dataset_outs[1] - num_sol[:, 1]))

for epoch in range(epochs):
  with tf.GradientTape() as tape:
    num_sol = net()
    loss_value = loss_func(num_sol)
  print("Epoch:", epoch, " loss:", loss_value.numpy())
  grads = tape.gradient(loss_value, args)
  optimizer.apply_gradients(zip(grads, args))

print("Learned parameters:", [args[i].numpy() for i in range(0, 4)])
num_sol = net()
x_num_sol = num_sol[:, 0].numpy()
y_num_sol = num_sol[:, 1].numpy()

x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)

plt.figure()
plt.plot(t_space, x_an_sol,'--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol,'--', linewidth=2, label='analytical y')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical x')
plt.plot(t_space, y_num_sol, linewidth=1, label='numerical y')
plt.title('Neural ODEs to fit params')
plt.xlabel('t')
plt.legend()
plt.show()
    Qui il link al codice su GitHub.

    I valori dei parametri ottenuti al termine dell'addrestramento sono i seguenti: $$ \left[\begin{matrix}a_1 \\ b_1 \\ c_1 \\ d_1 \\ a_2 \\ b_2 \\ c_2 \\ d_2 \end{matrix} \right] = \left[\begin{matrix}1.5526739031012387 \\ 1.153349483970675 \\ -1.705896205847302 \\ 0.38685266435358123 \\ 1.0173442364137184 \\ 0.7136534371585501 \\ -0.9789359917976935 \\ 1.4237334700663127 \end{matrix} \right] $$ che sono ovviamente diversi dai valori dei parametri utilizzati per generare il dataset (passando tramite la soluzione analitica); però il sistema di equazioni ottenuto sostituendo i parametri formali con tali valori ottenuti dall'addestramento della rete neurale e risolvendolo numericamente questo ultimo sistema si ottiene una soluzione numerica che approssima abbastanza bene il dataset, come mostrato dalla figura:

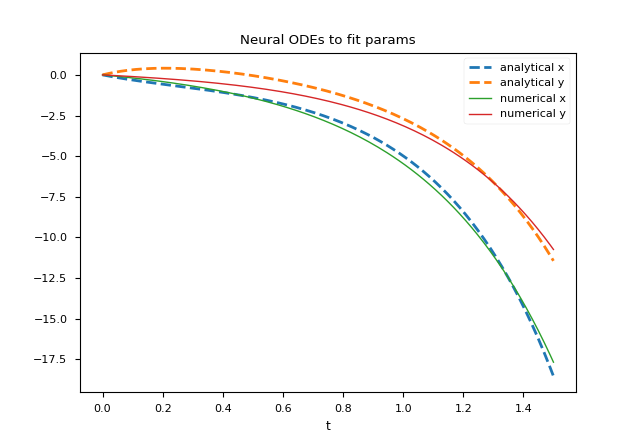
    Comparazione della soluzione numerica che approssima il dataset.

    Differenti strategie di addestramento consentono di ottenere diversi valori dei parametri e quindi una diversa soluzione numerica del sistema con una differente accuratezza.

    Citazioni

    @articleDBLP:journals/corr/abs-1806-07366,
  author    = {Tian Qi Chen and
               Yulia Rubanova and
               Jesse Bettencourt and
               David Duvenaud},
  title     = {Neural Ordinary Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1806.07366},
  year      = {2018},
  url       = {http://arxiv.org/abs/1806.07366},
  archivePrefix = {arXiv},
  eprint    = {1806.07366},
  timestamp = {Mon, 22 Jul 2019 14:09:23 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-1806-07366.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}

    Download del codice completo

    Il codice completo è disponibile su GitHub.
    Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
    Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.