Esperimenti con Neural ODEs in Julia

Neural Ordinary Differential Equations (abbreviato Neural ODEs) è un paper che introduce una nuova famiglia di reti neurali in cui alcuni strati nascosti (o anche l'unico strato nei casi più semplici) sono implementati con un risolutore di equazioni differenziali ordinarie.
Questo post mostra tre esempi scritti in Julia che utilizzano alcune idee descritte nel paper Neural ODEs per mostrare possibili soluzioni nei seguenti scenari:

• Esperimento #1: addestrare un sistema di ODE per soddisfare un obiettivo.
• Esperimento #2: calcolare il forecast di un sistema di serie temporali descritto da una legge differenziale.
• Esperimento #3: approssimare una funzione con MLP e Neural ODEs

Convenzioni

In questo post le convenzioni adoperate sono le seguenti:

• $t$ è la variabile indipendente
• $x$ è la funzione incognita
• $y$ è la seconda funzione incognita
• $x$ e $y$ sono da intendersi funzioni di $t$, quindi $x=x(t)$ e $y=y(t)$, ma l'uso di questa notazione compatta, oltre ad avere una maggiore leggibilità a livello matematico rende più agevole la "traduzione" in codice dell'equazione
• $x'$ è la derivata prima di x rispetto a $t$ e naturalmente $y'$ è la derivata prima di y rispetto a $t$

Esperimento #1: addestrare un sistema di ODE per soddisfare un obiettivo

Un percettrone multistrato (abbreviato MLP) è uno strumento opportuno per imparare una relazione non lineare tra input e output di cui non si conosce la legge.
Ci sono casi invece in cui si ha conoscenza a priori della legge che correla gli input e gli output, ad esempio nella forma di un sistema parametrico di equazioni differenziali: in questa situazione una rete neurale di tipo MLP non consente di utilizzare tale conoscenza mentre una rete di tipo Neural ODEs sì.

Lo scenario di applicazione

Lo scenario di applicazione è il seguente:

• Un dataset che contenga gli input e gli output.
• Una legge che associ input e output in forma di sistema parametrico di equazioni differenziali.

• Determinare opportuni valori dei parametri affiché il sistema ottenuto sostituendo i parametri formali con i valori determinati approssimi al meglio la mappatura tra input e output.

Il problema da risolvere

Sia dato il seguente sistema parametrico di due equazioni differenziali ordinarie con valori iniziali che rappresenta la legge che descrive il comportamento di un ipotetico sistema dinamico: $$ \begin{equation} \begin{cases} x' = a_1x + b_1y + c_1e^{-d_1t} \\ y'= a_2x + b_2y + c_2e^{-d_2t} \\ x(0)=0 \\ y(0)=0 \end{cases} \end{equation} $$ Ovviamente questa è una demo il cui scopo è provare la bontà del metodo, quindi per preparare il dataset si fissino arbitrariamente gli otto valori dei parametri, ad esempio questi: $$ \left[\begin{matrix}a_1 \\ b_1 \\ c_1 \\ d_1 \\ a_2 \\ b_2 \\ c_2 \\ d_2 \end{matrix} \right] = \left[\begin{matrix}1.11 \\ 2.43 \\ -3.66 \\ 1.37 \\ 2.89 \\ -1.97 \\ 4.58 \\ 2.86 \end{matrix} \right] $$ e sapendo che con tali valori dei parametri la soluzione analitica è la seguente: $$ \begin{equation} \begin{array}{l} x(t) = \\ \;\; -1.38778 \cdot 10^{-17} \; e^{-8.99002 t} - \\ \;\; 2.77556 \cdot 10^{-17} \; e^{-7.50002 t} + \\ \;\; 3.28757 \; e^{-3.49501 t} - \\ \;\; 3.18949 \; e^{-2.86 t} + \\ \;\; 0.258028 \; e^{-1.37 t} - \\ \;\; 0.356108 \; e^{2.63501 t} + \\ \;\; 4.44089 \cdot 10^{-16} \; e^{3.27002 t} + \\ \;\; 1.11022 \cdot 10^{-16} \; e^{4.76002 t} \\ \\ y(t) = \\ \;\; -6.23016 \; e^{-3.49501 t} + \\ \;\; 5.21081 \; e^{-2.86 t} + \\ \;\; 1.24284 \; e^{-1.37 t} - \\ \;\; 0.223485 \; e^{2.63501 t} + \\ \;\; 2.77556 \cdot 10^{-17} \; e^{4.76002 t} \\ \end{array} \end{equation} $$ (verificabile online tramite Wolfram Alpha) si è in grado di preparare il dataset: l'input è un intervallo discretizzato del tempo da $0$ a $1.5$ passo $0.01$, mentre l'output è costituito dalle soluzioni analitiche $x=x(t)$ e $y=y(t)$ per ogni $t$ appartenente all'input.
Una volta preparato il dataset ci si dimentichi dei valori dei parametri e della soluzione analitica e ci si pone il problema di come addestrare una rete neurale per determinare un opportuno set di valori per gli otto parametri per approssimare al meglio la mappatura non lineare tra input e output del dataset.

L'implementazione della soluzione

Il sistema parametrico di equazioni differenziali è già scritto in forma esplicita e in Julia con DifferentialEquations si implementa così:

function parametric_ode_system!(du,u,p,t)
  x, y = u
  a1, b1, c1, d1, a2, b2, c2, d2 = p
  du[1] = dx = a1*x + b1*y + c1*exp(-d1*t)
  du[2] = dy = a2*x + b2*y + c2*exp(-d2*t)
end

• Input: $t \in [0, 1.5]$ passo di discretizzazione $0.01$
• Condizioni al contorno: $x(0)=0; y(0)=0$
• Valori iniziali del parametri qualsiasi; per comodità qui si impostano tutti uguali a $1$

tbegin=0.0
tend=1.5
tstep=0.01
trange = tbegin:tstep:tend
u0 = [0.0,0.0]
tspan = (tbegin,tend)
p = ones(8)

prob = ODEProblem(parametric_ode_system!, u0, tspan, p)

function net()
    solve(prob, Tsit5(), p=p, saveat=trange)
end

• Ottimizzatore: ADAM
• Learning rate: $0.05$
• Numero di epoche: $1000$
• Funzione di loss: somma dei quadrati delle differenze

epochs = 1000
learning_rate = 0.05
data = Iterators.repeated((), epochs)
opt = ADAM(learning_rate)
callback_func = function ()
  #.......
end
fparams = Flux.params(p)
Flux.train!(loss_func, fparams, data, opt, cb=callback_func)

using Flux, DiffEqFlux, DifferentialEquations, Plots

function parametric_ode_system!(du,u,p,t)
  x, y = u
  a1, b1, c1, d1, a2, b2, c2, d2 = p
  du[1] = dx = a1*x + b1*y + c1*exp(-d1*t)
  du[2] = dy = a2*x + b2*y + c2*exp(-d2*t)
end

true_params = [1.11, 2.43, -3.66, 1.37, 2.89, -1.97, 4.58, 2.86]

an_sol_x(t) =
  -1.38778e-17 * exp(-8.99002 * t) -
  2.77556e-17 * exp(-7.50002 * t) +
  3.28757 * exp(-3.49501 * t) -
  3.18949 * exp(-2.86 * t) +
  0.258028 * exp(-1.37 * t) -
  0.356108 * exp(2.63501 * t) +
  4.44089e-16 * exp(3.27002 * t) +
  1.11022e-16 * exp(4.76002 * t)
an_sol_y(t) =
  -6.23016 * exp(-3.49501 * t) +
  5.21081 * exp(-2.86 * t) +
  1.24284 * exp(-1.37 * t) -
  0.223485 * exp(2.63501 * t) +
  2.77556e-17 * exp(4.76002 * t)

tbegin=0.0
tend=1.5
tstep=0.01
trange = tbegin:tstep:tend
u0 = [0.0,0.0]
tspan = (tbegin,tend)
p = ones(8)

prob = ODEProblem(parametric_ode_system!, u0, tspan, p)

function net()
    solve(prob, Tsit5(), p=p, saveat=trange)
end

dataset_outs = [an_sol_x.(trange), an_sol_y.(trange)]
function loss_func()
  pred = net()
  sum(abs2, dataset_outs[1] .- pred[1,:]) +
  sum(abs2, dataset_outs[2] .- pred[2,:])
end

epochs = 1000
learning_rate = 0.05
data = Iterators.repeated((), epochs)
opt = ADAM(learning_rate)
callback_func = function ()
  println("loss: ", loss_func())
end
fparams = Flux.params(p)
Flux.train!(loss_func, fparams, data, opt, cb=callback_func)

predict_prob = ODEProblem(parametric_ode_system!, u0, tspan, p)
predict_sol = solve(prob, Tsit5(), saveat=trange)
x_predict_sol = [u[1] for u in predict_sol.u]
y_predict_sol = [u[2] for u in predict_sol.u]

println("Learned parameters:", p)

plot(trange, dataset_outs[1],
    linewidth=2, ls=:dash,
    title="Neural ODEs to fit params",
    xaxis="t",
    label="dataset x(t)",
    legend=true)
plot!(trange, dataset_outs[2],
    linewidth=2, ls=:dash,
    label="dataset y(t)")
plot!(predict_sol.t, x_predict_sol,
    linewidth=1,
    label="predicted x(t)")
plot!(predict_sol.t, y_predict_sol,
    linewidth=1,
    label="predicted y(t)")

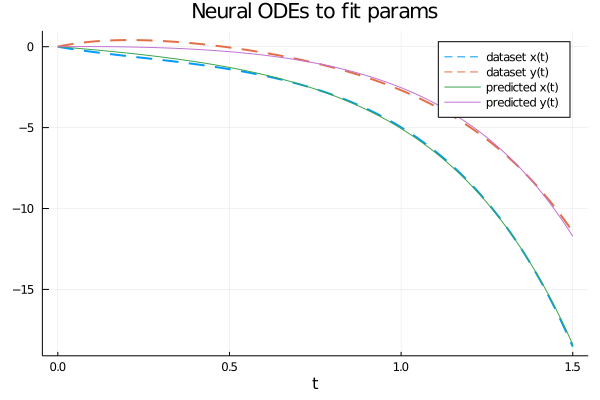
Differenti strategie di addestramento consentono di ottenere diversi valori dei parametri e quindi una diversa soluzione numerica del sistema con una differente accuratezza.

Esperimento #2: calcolare il forecast di un sistema di serie temporali descritto da una legge differenziale

Ci sono varie tassonomie di reti neurali black-box per calcolare il forecast di serie temporali (si veda il post Forecast di una serie temporale univariata ed equispaziata con TensorFlow su questo sito web) che sono adatte quando non si ha conoscenza a priori della legge matematica che descriva il comporamento delle serie temporali in input.
Quando invece si ha conoscenza a priori della legge differenziale che regoli l'evoluzione delle derivate delle serie temporali (ad esempio nella forma di un sistema parametrico di equazioni differenziali) una rete di tipo Neural ODE diventa lo strumento giusto per calcolare il forecast in modo efficiente e accurato.

Lo scenario di applicazione

Lo scenario di applicazione è il seguente:

• Un dataset che contenga un set di serie temporali interdipendenti.
• Una legge che regoli l'evoluzione delle derivate delle serie temporali nel tempo sotto forma di sistema parametrico di equazioni differenziali.

• 1. Addestrare una rete neurale di tipo NeuralODE per imparare il valore dei parametri del sistema di ODE a partire dalle serie temporali in input.
• 2. Utilizzare il sistema imparato per calcolare il forecast, quindi le predizioni con tempo posteriore a quello delle serie temporali iniziali.

Il problema da risolvere

Sia dato il seguente sistema parametrico di due equazioni differenziali ordinarie con valori iniziali che rappresenta la legge che descrive l'evoluzione delle derivate di una coppia di serie temporali interdipendenti: $$ \begin{equation} \begin{cases} \left[\begin{matrix} x' & y' \end{matrix} \right] = \left[\begin{matrix} \sin 2x + \cos 2y \\ \sin 2x + \cos 2y \end{matrix} \right] ^ \dag \left[\begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right] \\ x(0)=x_0 \\ y(0)=y_0 \end{cases} \end{equation} $$ Ovviamente questa è una demo il cui scopo è provare la bontà del metodo, quindi per preparare il dataset si fissino arbitrariamente i valori dei quattro parametri e le due condizioni iniziali: $$ A = \left[\begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right] = \left[\begin{matrix}-0.15 & 2.10 \\ -2.10 & -0.10 \end{matrix} \right] $$ $$ \begin{equation} \begin{cases} x(0)=2.5 \\ y(0)=0.5 \end{cases} \end{equation} $$ in modo da poter creare il dataset della coppia delle vere serie temporali: il tempo viene discretizzato in modo arbitrario da $0$ a $4$ con un numero di $51$ valori discreti, mentre le serie temporali $x(t)$ e $y(t)$ sono costruite risolvendo il sistema di equazioni differenziali ottenuto usando la matrice A dei parametri specifici nel sistema parametrico di cui sopra, insieme alle condizioni iniziali scelte arbitrariamente.
Una volta preparato il dataset (che nel mondo reale può essere ottenuto eseguendo delle vere misurazioni) ci si dimentichi dei valori dei parametri (che quindi diventeranno sconosciuti) e ci si ponga un duplice problema:

• come addestrare una rete neurale che incorpori la legge nota per imparare il sistema a parametri sconosciuti al fine di approssimare al meglio le serie temporali iniziali?
• come utilizzare tale rete neurale una volta addestrata per predire valori futuri (il forecast, appunto)?

L'implementazione della soluzione

La legge matematica del sistema di cui sopra in Julia si implementa così:

math_law(u) = sin.(2. * u) + cos.(2. * u)

function true_ode(du,u,p,t)
    true_A = [-0.15 2.10; -2.10 -0.10]
    du .= ((math_law(u))'true_A)'
end

tbegin = 0.0
tend = 4.0
datasize = 51
t = range(tbegin,tend,length=datasize)
u0 = [2.5; 0.5]
tspan = (tbegin,tend)
trange = range(tbegin,tend,length=datasize)
prob = ODEProblem(true_ode, u0, tspan)
dataset_ts = Array(solve(prob, Tsit5(), saveat=trange))

dudt = Chain(u -> math_law(u),
             Dense(2, 50, tanh),
             Dense(50, 2))

reltol = 1e-7
abstol = 1e-9
n_ode = NeuralODE(dudt, tspan, Tsit5(), saveat=trange, reltol=reltol,abstol=abstol)
ps = Flux.params(n_ode.p)

• Ottimizzatore: ADAM
• Learning rate: $0.01$
• Numero di epoche: $400$
• Funzione di loss: somma dei quadrati delle differenze

function loss_n_ode()
  pred = n_ode(u0)
  loss = sum(abs2, dataset_ts1,: .- pred1,:) +
         sum(abs2, dataset_ts2,: .- pred2,:)
  loss
end

n_epochs = 400
learning_rate = 0.01
data = Iterators.repeated((), n_epochs)
opt = ADAM(learning_rate)

cb = function ()
  loss = loss_n_ode()
  println("Loss: ", loss)
end

println();
cb()

Flux.train!(loss_n_ode, ps, data, opt, cb=cb)]

• Tempo di inizio: coincidente con il tempo di fine della serie temporale di input, quindi $4$.
• Tempo di fine: tempo di inizio del forecast più una quantitè di tempo a piacere, diciamo 5, quindi $4+5$, cioè $9$.
• Numero di valori temporali: 351 (quindi molti più punti e molto più fitti rispetto alle serie temporali di input).
• Condizione iniziale: gli ultimi valori delle serie temporali di input.

tbegin_forecast = tend
tend_forecast = tbegin_forecast + 5.0
tspan_forecast = (tbegin_forecast, tend_forecast)
datasize_forecast = 351
trange_forecast = range(tspan_forecast[1], tspan_forecast[2], length=datasize_forecast)
u0_forecast = [dataset_ts[1,datasize], dataset_ts[2,datasize]]

tbegin_forecast = tend
tend_forecast = tbegin_forecast + 5.0
tspan_forecast = (tbegin_forecast, tend_forecast)
datasize_forecast = 351
trange_forecast = range(tspan_forecast[1], tspan_forecast[2], length=datasize_forecast)
u0_forecast = [dataset_ts[1,datasize], dataset_ts[2,datasize]]

n_ode_forecast = NeuralODE(
  n_ode.model, tspan_forecast;
  p=n_ode.p, saveat=trange_forecast, reltol=reltol, abstol=abstol)
forecast = n_ode_forecast(u0_forecast)

• Le due serie temporali originali in input.
• Le due serie temporali così come le approssima la rete neurale dopo l'addestramento.
• La proiezione nel futuro delle due serie temporali (forecast).

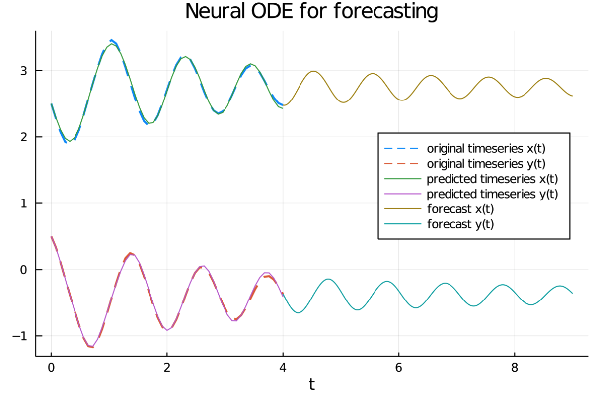
Dal grafico si evince chiaramente che la rete neurale ha imparato bene le proprietà di oscillazione e smorzatura delle due serie e riesce a proiettarle nel fututo.

Si noti soprattutto il concetto di profondità continua tipico delle NeuralODEs, infatti mentre nelle classiche reti neurali il passo di discretizzazione delle serie temporali di input è lo stesso nel forecast, con le NeuralODEs invece l'array dei tempi con cui calcolare la predizione può essere arbitrariamente fitto, proprio perché il risolutore di equazioni differenziali dentro la rete neurale, per sua propria natura, lavora nel continuo e trasmette questa proprietà a tutta la rete.

Qui il link al codice completo su GitHub.

Esperimento #3: approssimare una funzione con MLP e Neural ODEs

Anche se il paper Neural ODEs non cita esplicitamente l'approssimazione delle funzioni con gli MLP (i percettroni multistrato, dall'inglese Multi Layer Perceptron) un campo di applicazione che possa trarre beneficio dalle Neural ODE, tuttavia è interessante comunque vedere come costruire una rete neurale costituita da un MLP e da un layer a profondità continua realizzato tramite un layer di tipo Neural ODE.
L'esperimento ha due obiettivi:

• Mostrare come si definisce un MLP utilizzando FastChain e FastDense definiti in DiffEqFlux (a differenza degli esperimenti precedenti in cui si è adoperato Chain e Dense definiti Flux) senza uso di Neural ODE per approssimare una funzione.
• Innestare un layer Neural ODE sulla rete di tipo MLP e mostrare le modifiche necessarie da apportare al codice per utilizzare questa combinazione di MLP e Neural ODE per approssimare la stessa funzione.

Lo scenario di applicazione

Lo scenario di applicazione è il seguente:

• Un dataset che contenga una mappatura di valori reali di input (variabile $t$, il tempo) con valori reali di output (variabile $y$).
  Il dataset è creato in modo sintetico tramite una funzione generatrice $y=y(t)$.

• Approssimare con una rete neurale la mappatura input $\to$ output rappresentata dal dataset.

Il problema da risolvere

Sia data la seguente funzione generatrice del dataset (che diventa quindi la funzione da approssimare): $$ y(t) = \ln{(1 + t)} - 3 \sqrt {t} \:\:\:\: t \in [0,4] $$ dove il tempo $t$ viene discretizzato da $0$ a $4$ con un numero di $51$ valori discreti; naturalmente nel mondo reale il dataset è ottenuto eseguendo delle vere misurazioni sul campo, qui invece è generato da una funzione generatrice a scopo dimostrativo.
Il problema da risolvere, come già detto, è addestrare una rete neurale per approssimare tale funzione addestrando la rete neurale (dapprima un MLP puro, poi un MLP combinato con un layer Neural ODE) sul dataset generato tramite la funzione generatrice di cui sopra.

L'implementazione della soluzione senza Neural ODE

Gli using necessari all'intero programma sono i seguenti:

using Plots
using Flux
using DiffEqFlux

tbegin = 0.0
tend = 4.0
datasize = 51
dataset_in = range(tbegin, tend, length=datasize)
dataset_out = log.(1 .+ dataset_in) .- 3 * sqrt.(dataset_in)

function neural_network(data_dim)
    fc = FastChain(FastDense(data_dim, 64, swish),
                  FastDense(64, 32, swish),
                  FastDense(32, data_dim))
end

nn = neural_network(1)
theta = initial_params(nn)

• Numero di dimensione del layer di input: 1
• Numero di dimensione del layer di output: 1
• Layer nascosti: 2 layer, uno da 64 neuroni e uno da 32
• Funzione di attivazione: swish

predict(t, p) = nn(t', p)'

loss(p) = begin
  yhat = predict(dataset_in, p)
  l = Flux.mse(yhat, dataset_out)
end

• Ottimizzatore: ADAMW
• Learning rate: $0.01$
• Numero di epoche: $1500$
• Funzione di loss: MSE

learning_rate=1e-2
opt = ADAMW(learning_rate)
epochs = 1500

function cb_train(theta, loss)
    println("Loss: ", loss)
    false
end

res_train = DiffEqFlux.sciml_train(
    loss, theta, opt,
    maxiters = epochs,
    cb = cb_train)
    
y_pred = predict(dataset_in, res_train.minimizer)

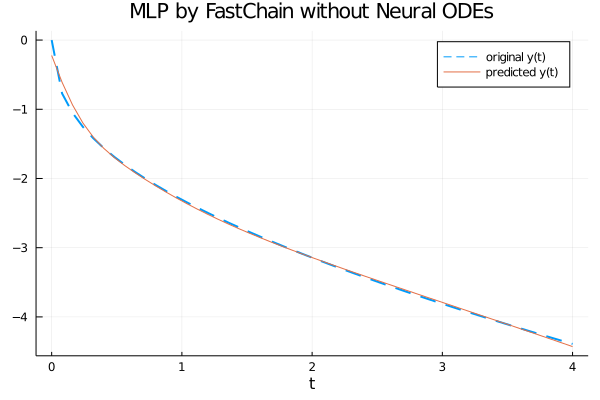
Dal grafico si evince chiaramente che la rete neurale approssima bene la funzione generatriche nell'intervallo $[0, 4]$.

Qui il link al codice completo su GitHub.

L'implementazione della soluzione con Neural ODE

Gli using necessari all'intero programma sono i seguenti:

using Plots
using Flux
using DiffEqFlux
using OrdinaryDiffEq

tbegin = 0.0
tend = 4.0
datasize = 51
dataset_in = range(tbegin, tend, length=datasize)
dataset_out = log.(1 .+ dataset_in) .- 3 * sqrt.(dataset_in)

function neural_ode(data_dim; saveat = dataset_in)
    fc = FastChain(FastDense(data_dim, 64, swish),
                  FastDense(64, 32, swish),
                  FastDense(32, data_dim))

    n_ode = NeuralODE(
            fc,
            (minimum(dataset_in), maximum(dataset_in)),
            Tsit5(),
            saveat = saveat,
            abstol = 1e-9, reltol = 1e-9)
end

n_ode = neural_ode(1)
theta = n_ode.p

predict(p) = n_ode(dataset_out[1:1], p)'

loss(p) = begin
  yhat = predict(p)
  l = Flux.mse(yhat, dataset_out)
end

• Ottimizzatore: ADAMW
• Learning rate: $0.01$
• Numero di epoche: $500$
• Funzione di loss: MSE

learning_rate=1e-2
opt = ADAMW(learning_rate)
epochs = 500

function cb_train(theta, loss)
    println("Loss: ", loss)
    false
end

res_train = DiffEqFlux.sciml_train(
    loss, theta, opt,
    maxiters = epochs,
    cb = cb_train)

y_pred = predict(res_train.minimizer)

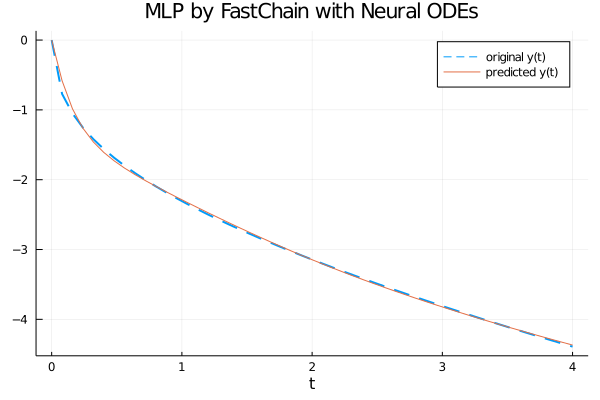
Dal grafico si evince chiaramente che la rete neurale con un layer Neural ODE approssima bene la funzione generatriche nell'intervallo $[0, 4]$.

Qui il link al codice completo su GitHub.

Citazioni

@articleDBLP:journals/corr/abs-1806-07366,
  author    = {Tian Qi Chen and
               Yulia Rubanova and
               Jesse Bettencourt and
               David Duvenaud},
  title     = {Neural Ordinary Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1806.07366},
  year      = {2018},
  url       = {http://arxiv.org/abs/1806.07366},
  archivePrefix = {arXiv},
  eprint    = {1806.07366},
  timestamp = {Mon, 22 Jul 2019 14:09:23 +0200},
  biburl    = {https://dblp.org/rec/journals/corr/abs-1806-07366.bib},
  bibsource = {dblp computer science bibliography, https://dblp.org}

@articleDBLP:journals/corr/abs-1902-02376,
  author    = {Christopher Rackauckas and
               Mike Innes and
               Yingbo Ma and
               Jesse Bettencourt and
               Lyndon White and
               Vaibhav Dixit},
  title     = {DiffEqFlux.jl - {A} Julia Library for Neural Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1902.02376},
  year      = {2019},
  url       = {https://arxiv.org/abs/1902.02376},
  archivePrefix = {arXiv},
  eprint    = {1902.02376},
  timestamp = {Tue, 21 May 2019 18:03:36 +0200},
  biburl    = {https://dblp.org/rec/bib/journals/corr/abs-1902-02376},
  bibsource = {dblp computer science bibliography, https://dblp.org}

Download del codice completo

Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.