Risolutori di equazioni differenziali ordinarie in Python
Questo post mostra l'utilizzo di alcuni risolutori di equazioni differenziali ordinarie (abbreviato ODE per Ordinary Differential Equation)
implementati da librerie per Python frequentemente adoperate nelle applicazioni scientifiche in generale e soprattutto nel machine learning e nel deep learning.
Le tecniche di risoluzione qui mostrate sono tecniche numeriche e non analitiche, in quanto questo sito si occupa di computazione.
Inoltre questo post è pubblicato sotto la categoria delle reti neurali: anche se non tutte le tecniche qui mostrate
adoperano tecnologie di deep learning, il suo scopo è quello essere propedeudico all'argomento sulla relazione tra le reti neurali e le equazioni differenziali.
Il post è organizzato come una sorta di Stele di Rosetta: sono presentati tre problemi,
precisamente una equazione del primo ordine, un sistema di due equazioni del primo ordine e una equazione del secondo ordine ciascuno con le proprie condizioni iniziali
(o condizioni di Cauchy, abbreviato IVP per Initial Value Problem) e a seguire la lista delle soluzioni degli stessi con le varie librerie utilizzate.
Di ciascun problema è nota anche la soluzione analitica e questo permette di confrontare la qualità delle soluzioni numeriche ottenute.
La Stele di Rosetta continua nel post Risolutori di equazioni differenziali ordinarie in Julia ove si mostra la soluzione degli stessi problemi in Julia.
Tutti i vari frammenti di codice descritti in questo post richiedono la versione 3 di Python e le librerie MatPlotLib e NumPy
mentre singolarmente richiedono una ulteriore libreria addizionale (ed eventuali sue dipendenze) in accordo con il risolutore utilizzato.
Per ottenere il codice si veda il paragrafo Download del codice completo in fondo a questo post.
Convenzioni
In questo post le convenzioni adoperate sono le seguenti:
- $t$ è la variabile indipendente
- $x$ è la funzione incognita
- $y$ è la seconda funzione incognita nel caso dei sistemi di due equazioni
- $x$ e $y$ sono da intendersi funzioni di $t$, quindi $x=x(t)$ e $y=y(t)$, ma l'uso di questa notazione compatta, oltre ad avere una maggiore leggibilità a livello matematico rende più agevole la "traduzione" in codice dell'equazione
- $x'$ è la derivata prima di $x$ rispetto a $t$ e naturalmente $y'$ è la derivata prima di y rispetto a $t$
- $x''$ è la derivata seconda di $x$ rispetto a $t$ e naturalmente $y''$ è la derivata seconda di $y$ rispetto a $t$
ODE del primo ordine con IVP
Sia dato il seguente problema di Cauchy:
$$ \begin{equation}
\begin{cases}
x'+x=\sin t + 3 \cos 2t
\\
x(0)=0
\end{cases}
\end{equation} $$
la cui soluzione analitica è:
$$ x(t) = \frac{1}{2} \sin t − \frac{1}{2} \cos t + \frac{3}{5} \cos 2t + \frac{6}{5} \sin 2t − \frac{1}{10}e^{-t} $$
verificabile online tramite Wolfram Alpha.
Le implementazioni dei risoluti qui di seguito richiedono che l'equazione differenziale sia scritta in forma esplicita nella forma $x'=F(x,t)$
e quindi diventa:
$$ x'=\sin t + 3 \cos 2t - x$$
Scipy
Scipy utilizza la funzione scipy.integrate.solve_ivp
per risolvere numericamente una equazione differenziale ordinaria del primo ordine con valore iniziale.
La forma esplicita dell'equazione di cui sopra in Python con NumPy si implementa così:
lambda t, x: np.sin(t) + 3. * np.cos(2. * t) - xQui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
scipy.integrate.solve_ivp:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
ode_fn = lambda t, x: np.sin(t) + 3. * np.cos(2. * t) - x
an_sol = lambda t : (1./2.) * np.sin(t) - (1./2.) * np.cos(t) + \
(3./5.) * np.cos(2.*t) + (6./5.) * np.sin(2.*t) - \
(1./10.) * np.exp(-t)
t_begin=0.
t_end=10.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = 0.
x_an_sol = an_sol(t_space)
method = 'RK45' #available methods: 'RK45', 'RK23', 'DOP853', 'Radau', 'BDF', 'LSODA'
num_sol = solve_ivp(ode_fn, [t_begin, t_end], [x_init], method=method, dense_output=True)
x_num_sol = num_sol.sol(t_space).T
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 1st order IVP solved by SciPy with method=' + method)
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
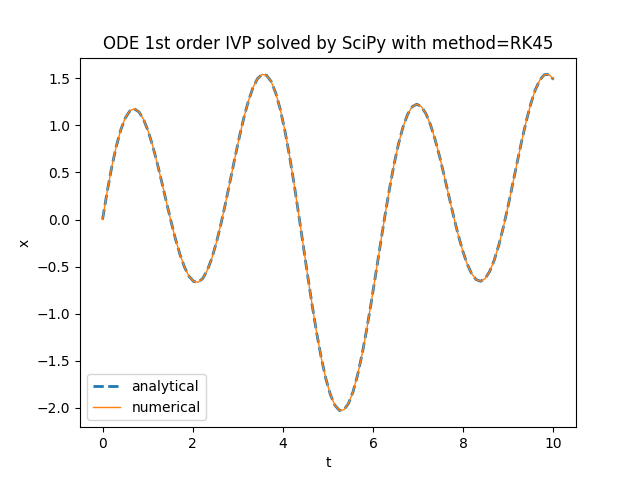
scipy.integrate.solve_ivp.TensorFlow Probability
TensorFlow Probability utilizza la classe tfp.math.ode.BDF
per risolvere numericamente una equazione differenziale ordinaria del primo ordine con valore iniziale.
La forma esplicita dell'equazione di cui sopra in Python con TensorFlow Probability si implementa così:
lambda t, x: tf.math.sin(t) + tf.constant(3.) * tf.math.cos(tf.constant(2.) * t) - xQui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
tfp.math.ode.BDF:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_probability as tfp
ode_fn = lambda t, x: tf.math.sin(t) + tf.constant(3.) * tf.math.cos(tf.constant(2.) * t) - x
an_sol = lambda t : (1./2.) * np.sin(t) - (1./2.) * np.cos(t) + \
(3./5.) * np.cos(2.*t) + (6./5.) * np.sin(2.*t) - \
(1./10.) * np.exp(-t)
t_begin=0.
t_end=10.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
t_init = tf.constant(t_begin)
x_init = tf.constant(0.)
x_an_sol = an_sol(t_space)
num_sol = tfp.math.ode.BDF().solve(ode_fn, t_init, x_init,
solution_times=tfp.math.ode.ChosenBySolver(tf.constant(t_end)) )
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(num_sol.times, num_sol.states, linewidth=1, label='numerical')
plt.title('ODE 1st order IVP solved by TensorFlow Probability with BDF')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
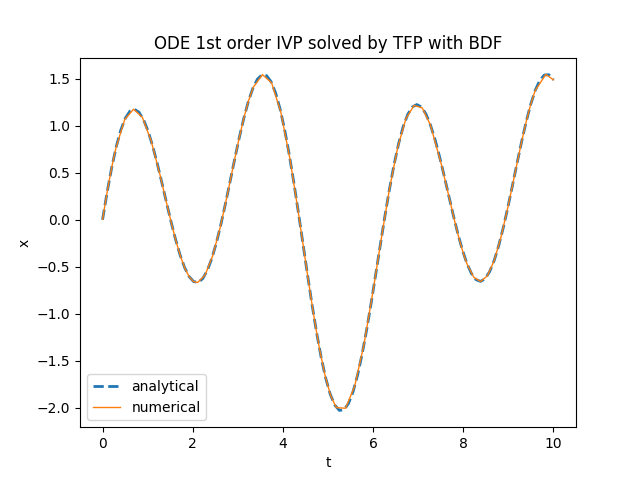
tfp.math.ode.BDFTorchDiffEq
TorchDiffEq utilizza la funzione torchdiffeq.odeint
per risolvere numericamente una equazione differenziale ordinaria del primo ordine con valore iniziale.
La forma esplicita dell'equazione di cui sopra in Python con Torch si implementa così:
lambda t, x: torch.sin(t) + 3. * torch.cos(2. * t) - xQui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
torchdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torchdiffeq import odeint
ode_fn = lambda t, x: torch.sin(t) + 3. * torch.cos(2. * t) - x
an_sol = lambda t : (1./2.) * np.sin(t) - (1./2.) * np.cos(t) + \
(3./5.) * np.cos(2.*t) + (6./5.) * np.sin(2.*t) - \
(1./10.) * np.exp(-t)
t_begin=0.
t_end=10.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = torch.tensor([0.])
x_an_sol = an_sol(t_space)
x_num_sol = odeint(ode_fn, x_init, torch.tensor(t_space))
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 1st order IVP solved by TorchDiffEq')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
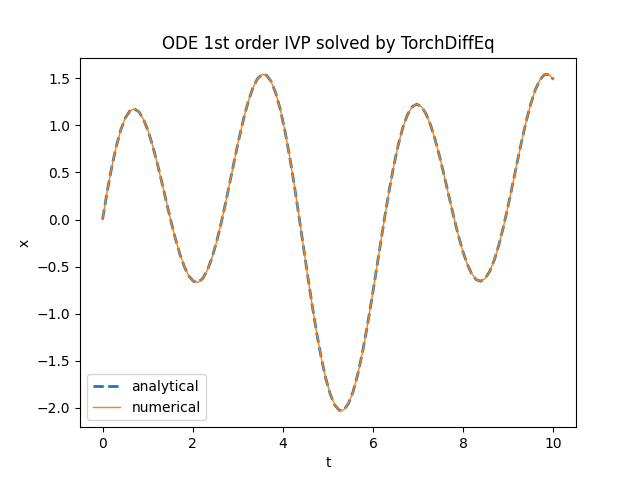
torchdiffeq.odeint.TensorFlowDiffEq
TensorFlowDiffEq è una libreria che replica con TensorFlow ciò che TorchDiffEq realizza con Torch.
TensorFlowDiffEq utilizza la funzione tfdiffeq.odeint per risolvere numericamente le equazioni differenziali ordinarie con valore iniziale.
La forma esplicita dell'equazione di cui sopra in Python con Tensorflow si implementa così:
lambda t, x: tf.math.sin(t) + 3. * tf.math.cos(2. * t) - xQui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
tfdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tfdiffeq import odeint
ode_fn = lambda t, x: tf.math.sin(t) + 3. * tf.math.cos(2. * t) - x
an_sol = lambda t : (1./2.) * np.sin(t) - (1./2.) * np.cos(t) + \
(3./5.) * np.cos(2.*t) + (6./5.) * np.sin(2.*t) - \
(1./10.) * np.exp(-t)
t_begin=0.
t_end=10.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = tf.constant([0.])
x_an_sol = an_sol(t_space)
x_num_sol = odeint(ode_fn, x_init, tf.constant(t_space))
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 1st order IVP solved by TensorFlowDiffEq')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
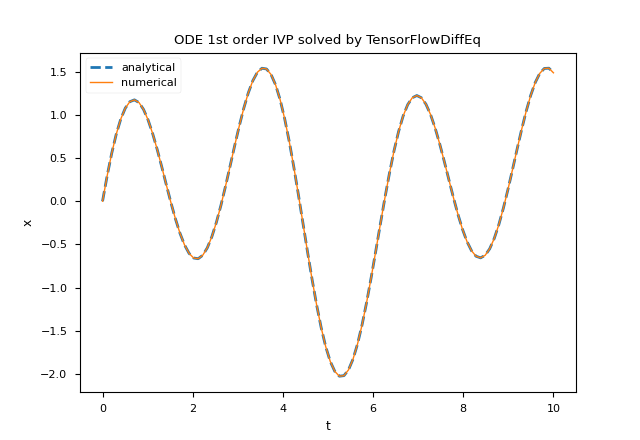
tfdiffeq.odeint.NeuroDiffEq
NeuroDiffEq è una libreria che utilizza una rete neurale implementata tramite PyTorch
per risolvere numericamente una equazione differenziale del primo ordine con valore iniziale.
Il risolutore NeuroDiffEq presenta una serie di differenze rispetto ai precedenti risolutori. Innanzitutto l'equazione differenziale va rappresentata in forma implicita:
$$ \begin{equation}
x'+x-\sin t - 3 \cos 2t = 0
\end{equation} $$
inoltre la funzione diff(x, t, order) consente di indicare la derivata prima e infine la lambda (o la funzione) che rappresenta l'equazione ha la $t$ e la $x$ invertite di posizione.
Per quanto appena detto la forma implicita dell'equazione di cui sopra in Python con Torch e NeuroDiffEq si implementa così:
lambda x, t: diff(x, t, order=1) + x - torch.sin(t) - 3. * torch.cos(2. * t)La libreria NeuroDiffEq utilizza la funzione
neurodiffeq.ode.solve per eseguire l'approssimazione della soluzione dell'equazione;
tale funzione prende in input (opzionalmente) una rete neurale, l'algoritmo di training e altri iperparametri.Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
neurodiffeq.ode.solve
nell'intervallo $[0.0,2.0]$ con le seguenti impostazioni:
- rete neurale Fully Connected (abbreviata FC, detta anche MLP per multilayer perceptron) con 6 layer, 50 neuroni per layer e Tanh quale funzione di attivazione;
- algoritmo di ottimizzazione SGD con learing rate impostato a 0.001;
- batch size uguale a 30, numero massimo di epoche 1000, flag best model impostato a True.
import numpy as np
import matplotlib.pyplot as plt
import torch
from neurodiffeq import diff
from neurodiffeq.ode import solve
from neurodiffeq.ode import IVP
from neurodiffeq.ode import Monitor
import neurodiffeq.networks as ndenw
ode_fn = lambda x, t: diff(x, t, order=1) + x - torch.sin(t) - 3. * torch.cos(2. * t)
an_sol = lambda t : (1./2.) * np.sin(t) - (1./2.) * np.cos(t) + \
(3./5.) * np.cos(2.*t) + (6./5.) * np.sin(2.*t) - \
(1./10.) * np.exp(-t)
t_begin=0.
t_end=2.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = IVP(t_0=t_begin, x_0=0.0)
x_an_sol = an_sol(t_space)
net = ndenw.FCNN(n_hidden_layers=6, n_hidden_units=50, actv=torch.nn.Tanh)
optimizer = torch.optim.SGD(net.parameters(), lr=0.001)
num_sol, loss_sol = solve(ode_fn, x_init, t_min=t_begin, t_max=t_end,
batch_size=30,
max_epochs=1000,
return_best=True,
net=net,
optimizer=optimizer,
monitor=Monitor(t_min=t_begin, t_max=t_end, check_every=10))
x_num_sol = num_sol(t_space, as_type='np')
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 1st order IVP solved by NeuroDiffEq')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
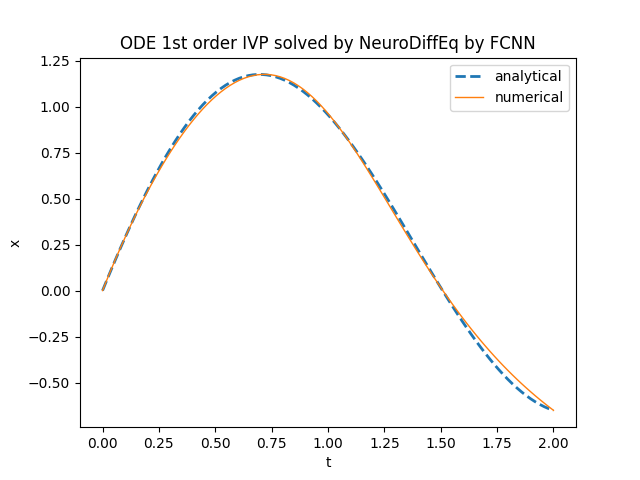
neurodiffeq.ode.solve.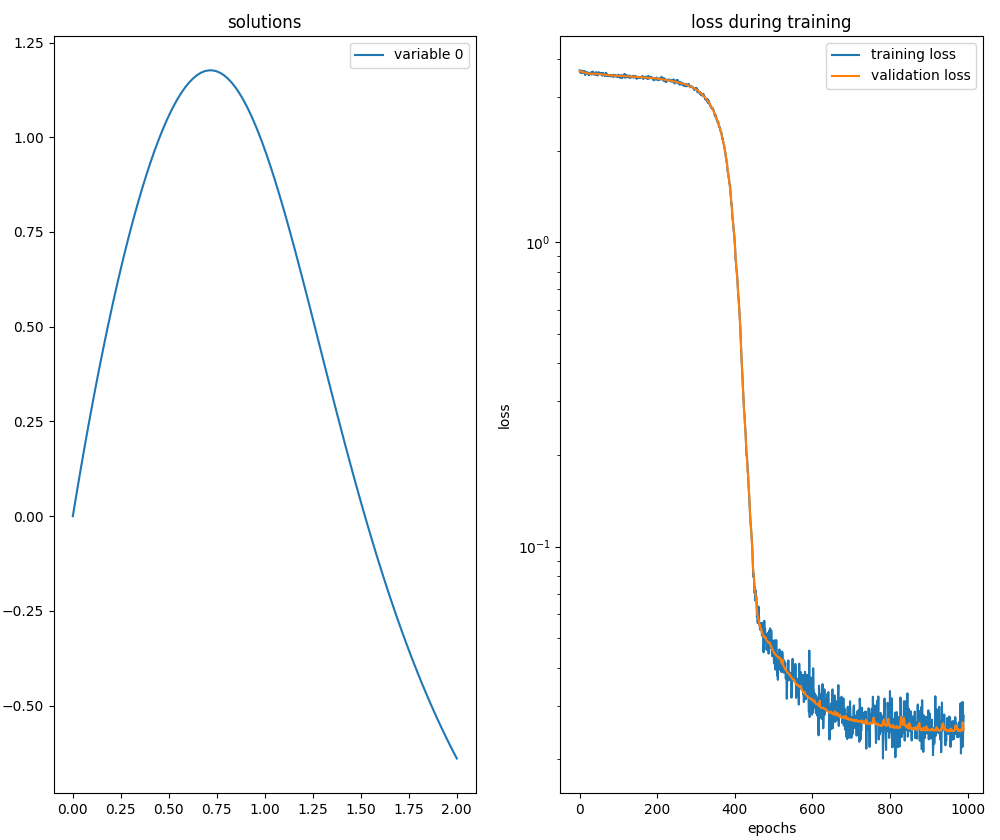
neurodiffeq.ode.solve.Sistema di due ODE del primo ordine con IVP
Sia dato il seguente sistema di due equazioni differenziali ordinarie con valori iniziali:
$$ \begin{equation}
\begin{cases}
x' + x − y = 0
\\
y' - 4x + y = 0
\\
x(0)=2
\\
y(0)=0
\end{cases}
\end{equation} $$
la cui soluzione analitica è:
$$ \begin{equation}
\begin{cases}
x(t) = e^t + e^{-3 t}
\\
y(t) = 2 e^t - 2 e^{-3 t}
\end{cases}
\end{equation} $$
verificabile online tramite Wolfram Alpha.
Le implementazioni dei risoluti qui di seguito richiedono che le equazioni differenziali siano scritta in forma esplicita nelle forme $x'=F_1(x,y,t)$ e $y'=F_2(x,y,t)$
e quindi le due equazioni diventano:
$$ \begin{equation}
\begin{cases}
x' = y - x
\\
y' = 4x - y
\end{cases}
\end{equation} $$
e in forma matriciale:
$$\left[\begin{matrix} x' \\ y' \end{matrix} \right] = \left[\begin{matrix} -1 & 1 \\ 4 & -1 \end{matrix} \right] \left[\begin{matrix} x \\ y \end{matrix} \right] $$
Scipy
Scipy utilizza la funzione scipy.integrate.solve_ivp
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali.
La forma esplicita della coppia di equazioni di cui sopra in Python con NumPy si implementa così:
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return [dx_dt, dy_dt]Alternativamente, il sistema rappresentato in forma matriciale in Python con Scipy si implementa così:
A = [[-1., 1.],
[4., -1.]]
ode_sys = lambda t, XY : A @ XYSi nota che il secondo argomento è un array di dimensione due, ovvero tante quanto il numero delle funzioni incognite.
Qui di seguito un esempio di codice Python che confronta la soluzione analitica del sistema con quella numerica ottenuta tramite
scipy.integrate.solve_ivp:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return [dx_dt, dy_dt]
an_sol_x = lambda t : np.exp(t) + np.exp(-3. * t)
an_sol_y = lambda t : 2. * np.exp(t) - 2. * np.exp(-3. * t)
t_begin=0.
t_end=5.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = 2.
y_init = 0.
x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)
method = 'RK45' #available methods: 'RK45', 'RK23', 'DOP853', 'Radau', 'BDF', 'LSODA'
num_sol = solve_ivp(ode_sys, [t_begin, t_end], [x_init, y_init], method=method, dense_output=True)
XY_num_sol = num_sol.sol(t_space)
x_num_sol = XY_num_sol[0].T
y_num_sol = XY_num_sol[1].T
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol, '--', linewidth=2, label='analytical y')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical x')
plt.plot(t_space, y_num_sol, linewidth=1, label='numerical y')
plt.title('System of 2 ODEs 1st order IVP solved by SciPy with method=' + method)
plt.xlabel('t')
plt.legend()
plt.show()
Qui il link per la variante matriciale su GitHub.
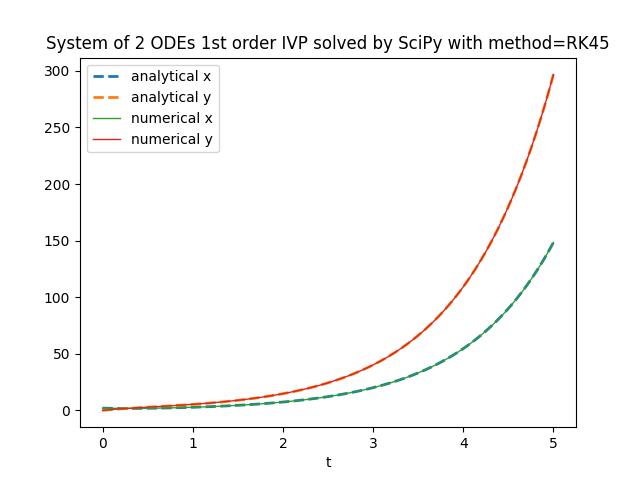
scipy.integrate.solve_ivp.TensorFlow Probability
TensorFlow Probability utilizza la classe tfp.math.ode.BDF
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali.
La forma esplicita della coppia di equazioni di cui sopra in Python con TensorFlow Probability si implementa così:
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return [dx_dt, dy_dt]Alternativamente, il sistema rappresentato in forma matriciale in Python con TensorFlow Probability si implementa così:
A = tf.constant([[-1., 1.], [4., -1.]])
ode_sys = lambda t, XY : tf.linalg.matvec(A, XY)Si nota che il secondo argomento è un array di dimensione due, ovvero tante quanto il numero delle funzioni incognite.
Qui di seguito un esempio di codice Python che confronta la soluzione analitica del sistema con quella numerica ottenuta tramite
tfp.math.ode.BDF:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_probability as tfp
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return [dx_dt, dy_dt]
an_sol_x = lambda t : np.exp(t) + np.exp(-3. * t)
an_sol_y = lambda t : 2. * np.exp(t) - 2. * np.exp(-3. * t)
t_begin=0.
t_end=5.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
t_init = tf.constant(t_begin)
x_init = tf.constant(2.)
y_init = tf.constant(0.)
x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)
num_sol = tfp.math.ode.BDF().solve(ode_sys, t_init, [x_init, y_init],
solution_times=tfp.math.ode.ChosenBySolver(tf.constant(t_end)) )
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol, '--', linewidth=2, label='analytical y')
plt.plot(num_sol.times, num_sol.states[0], linewidth=1, label='numerical x')
plt.plot(num_sol.times, num_sol.states[1], linewidth=1, label='numerical y')
plt.title('System of two ODEs 1st order IVP solved by TFP with BDF')
plt.xlabel('t')
plt.legend()
plt.show()
Qui il link per la variante matriciale su GitHub.
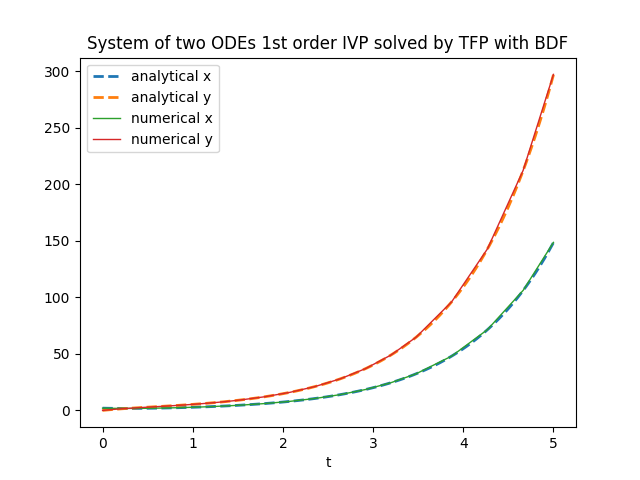
tfp.math.ode.BDFTorchDiffEq
TorchDiffEq utilizza la funzione torchdiffeq.odeint
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali.
La forma esplicita della coppia di equazioni di cui sopra in Python con Torch si implementa così:
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= torch.Tensor([- x + y])
dy_dt= torch.Tensor([4. * x - y])
return torch.cat([dx_dt, dy_dt])Alternativamente, il sistema rappresentato in forma matriciale in Python con Torch si implementa così:
A = torch.Tensor([[-1., 1.],
[4., -1.]])
ode_sys = lambda t, XY : A @ XYSi nota che il secondo argomento è un array di dimensione due, ovvero tante quanto il numero delle funzioni incognite.
Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
torchdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torchdiffeq import odeint
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= torch.Tensor([- x + y])
dy_dt= torch.Tensor([4. * x - y])
return torch.cat([dx_dt, dy_dt])
an_sol_x = lambda t : np.exp(t) + np.exp(-3. * t)
an_sol_y = lambda t : 2. * np.exp(t) - 2. * np.exp(-3. * t)
t_begin=0.
t_end=5.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = torch.Tensor([2.])
y_init = torch.Tensor([0.])
x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)
num_sol = odeint(ode_sys, torch.cat([x_init, y_init]), torch.Tensor(t_space)).numpy()
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol, '--', linewidth=2, label='analytical y')
plt.plot(t_space, num_sol[:,0], linewidth=1, label='numerical x')
plt.plot(t_space, num_sol[:,1], linewidth=1, label='numerical y')
plt.title('System of two ODEs 1st order IVP solved by TorchDiffEq')
plt.xlabel('t')
plt.legend()
plt.show()
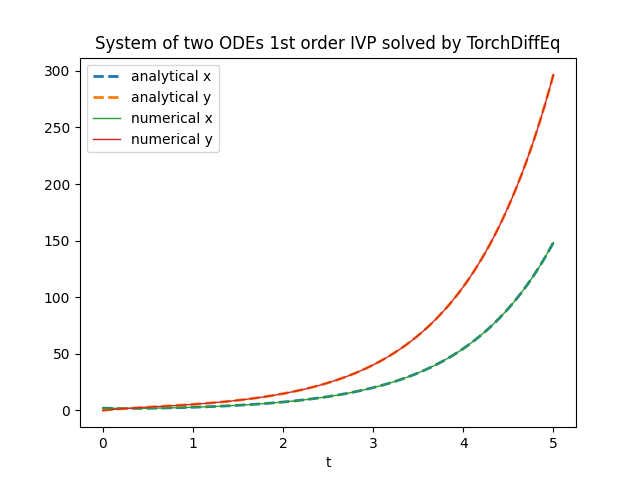
torchdiffeq.odeint.TensorFlowDiffEq
TensorFlowDiffEq utilizza la funzione tfdiffeq.odeint
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali.
La forma esplicita della coppia di equazioni di cui sopra in Python con TensorFlow si implementa così:
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return tf.stack([dx_dt, dy_dt])Alternativamente, il sistema rappresentato in forma matriciale in Python con TensorFlow si implementa così:
A = tf.constant([[-1., 1.],
[4., -1.]],
dtype=tf.float64)
ode_sys = lambda t, XY : A @ XYSi nota che il secondo argomento è un array di dimensione due, ovvero tante quanto il numero delle funzioni incognite.
Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
tfdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tfdiffeq import odeint
def ode_sys(t, XY):
x=XY[0]
y=XY[1]
dx_dt= - x + y
dy_dt= 4. * x - y
return tf.stack([dx_dt, dy_dt])
an_sol_x = lambda t : np.exp(t) + np.exp(-3. * t)
an_sol_y = lambda t : 2. * np.exp(t) - 2. * np.exp(-3. * t)
t_begin=0.
t_end=5.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = tf.constant([2.])
y_init = tf.constant([0.])
x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)
num_sol = odeint(
ode_sys,
tf.convert_to_tensor([x_init, y_init], dtype=tf.float64),
tf.constant(t_space)).numpy()
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol, '--', linewidth=2, label='analytical y')
plt.plot(t_space, num_sol[:,0], linewidth=1, label='numerical x')
plt.plot(t_space, num_sol[:,1], linewidth=1, label='numerical y')
plt.title('System of two ODEs 1st order IVP solved by TensorFlowDiffEq')
plt.xlabel('t')
plt.legend()
plt.show()
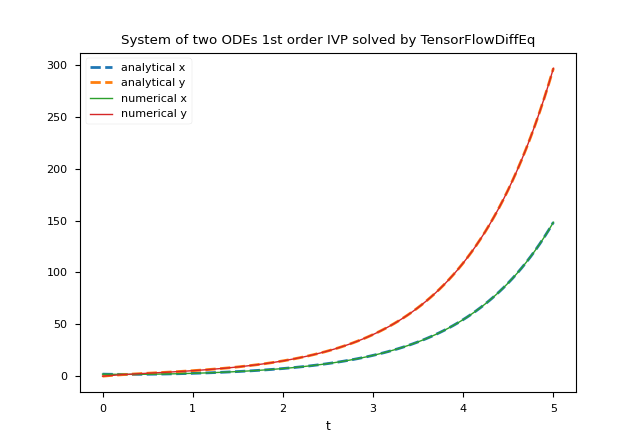
tfdiffeq.odeint.NeuroDiffEq
NeuroDiffEq è una libreria che utilizza una rete neurale implementata tramite PyTorch
per risolvere numericamente un sistema di equazioni differenziali del primo ordine con valori iniziali.
Come già detto sopra, il risolutore NeuroDiffEq presenta una serie di differenze rispetto ai precedenti risolutori. Innanzitutto il sistema di equazioni differenziali va rappresentata in forma implicita:
$$ \begin{equation}
\begin{cases}
x' + x − y = 0
\\
y' - 4x + y = 0
\end{cases}
\end{equation} $$
inoltre la funzione diff(x, t, order) consente di indicare la derivata prima di $x$ rispetto a $t$ e diff(y, t, order) la derivata prima di $y$ rispetto a $t$.
Infine la lambda (o la funzione) che rappresenta il sistema prende in ingresso tre parametri rispettivamente nell'ordine $x$, $y$ e $t$ e restituisce un array
con dimensione uguale al numero delle equazioni (in questo caso bidimensionale) per restituire il valore delle espressioni sinistre delle equazioni.
Per quanto appena detto la forma implicita del sistema di cui sopra in Python con Torch e NeuroDiffEq si implementa così:
lambda x, y, t: [diff(x, t, order=1) + x - y, diff(y, t, order=1) - 4. * x + y ]La libreria NeuroDiffEq utilizza la funzione
neurodiffeq.ode.solve_system per eseguire l'approssimazione della soluzione del sistema;
tale funzione prende in input (opzionalmente) una rete neurale, l'algoritmo di training e altri iperparametri.Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
neurodiffeq.ode.solve_system
nell'intervallo $[0.0,2.0]$ con le seguenti impostazioni:
- rete neurale Fully Connected (abbreviata FC, detta anche MLP per multilayer perceptron) con 3 layer, 50 neuroni per layer e SinActv quale funzione di attivazione;
- algoritmo di ottimizzazione Adam con learing rate impostato a 0.003;
- batch size uguale a 200, numero massimo di epoche 1200, flag best model impostato a True.
import numpy as np
import matplotlib.pyplot as plt
import torch
from neurodiffeq import diff
from neurodiffeq.ode import solve_system
from neurodiffeq.ode import IVP
from neurodiffeq.ode import Monitor
import neurodiffeq.networks as ndenw
ode_sys = lambda x, y, t: [diff(x, t, order=1) + x - y, diff(y, t, order=1) - 4. * x + y ]
an_sol_x = lambda t : np.exp(t) + np.exp(-3. * t)
an_sol_y = lambda t : 2. * np.exp(t) - 2. * np.exp(-3. * t)
t_begin=0.
t_end=2.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = IVP(t_0=t_begin, x_0=2.0)
y_init = IVP(t_0=t_begin, x_0=0.0)
x_an_sol = an_sol_x(t_space)
y_an_sol = an_sol_y(t_space)
batch_size=200
net = ndenw.FCNN(
n_input_units=1,
n_output_units=2,
n_hidden_layers=3,
n_hidden_units=50,
actv=ndenw.SinActv)
optimizer = torch.optim.Adam(net.parameters(), lr=0.003)
num_sol, history = solve_system(
ode_system=ode_sys,
conditions=[x_init, y_init],
t_min=t_begin,
t_max=t_end,
batch_size=batch_size,
max_epochs=1200,
return_best=True,
single_net = net,
optimizer=optimizer,
monitor=Monitor(t_min=t_begin, t_max=t_end, check_every=10))
num_sol = num_sol(t_space, as_type='np')
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical x')
plt.plot(t_space, y_an_sol, '--', linewidth=2, label='analytical y')
plt.plot(t_space, num_sol[0], linewidth=1, label='numerical x')
plt.plot(t_space, num_sol[1], linewidth=1, label='numerical y')
plt.title('System of two ODEs 1st order IVP solved by NeuroDiffEq')
plt.xlabel('t')
plt.legend()
plt.show()
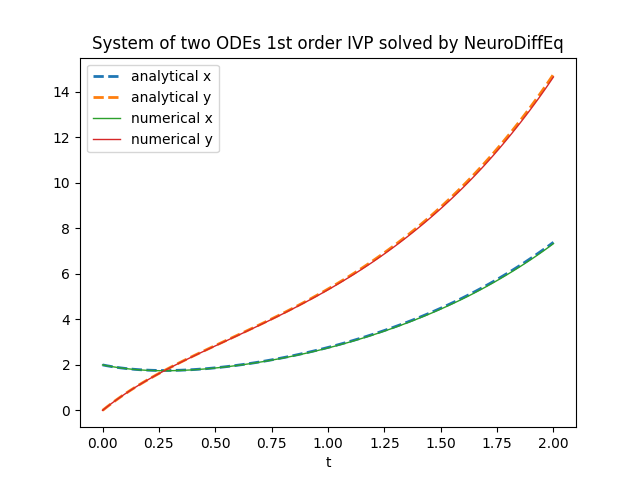
neurodiffeq.ode.solve_system.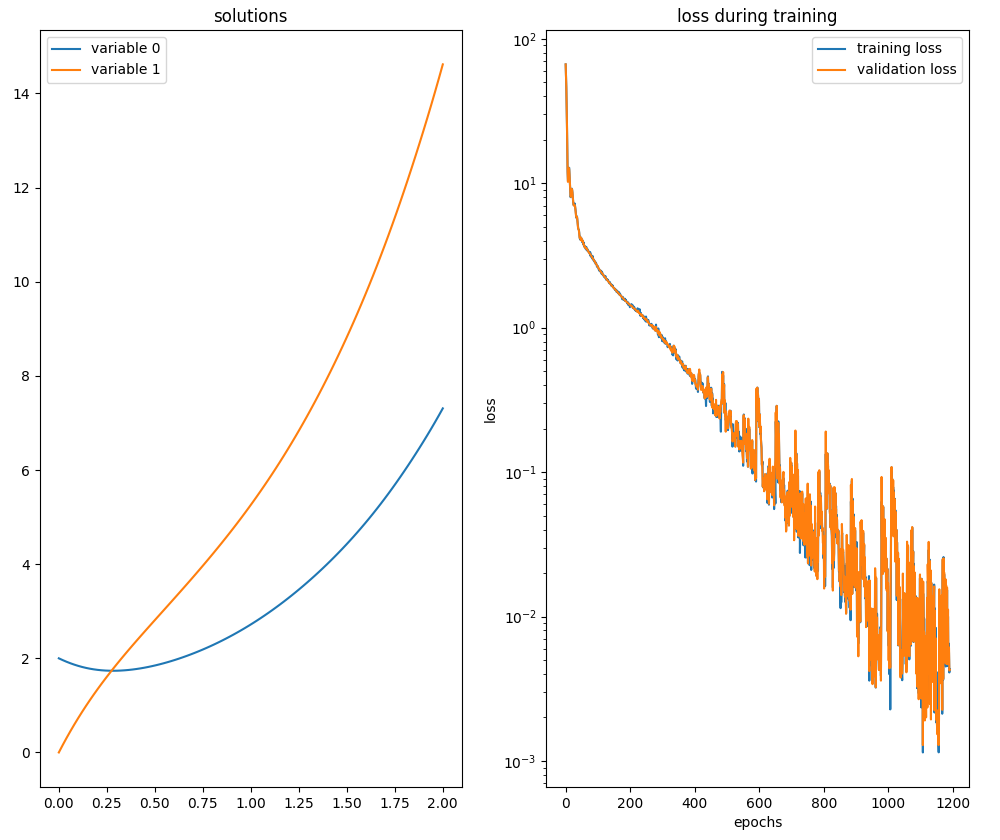
neurodiffeq.ode.solve_system.ODE del secondo ordine con IVP
Sia dato il seguente problema di Cauchy:
$$ \begin{equation}
\begin{cases}
x'' + x' + 2x = 0
\\
x(0)=1
\\
x'(0)=0
\end{cases}
\end{equation} $$
la cui soluzione analitica è:
$$ x(t) = e^{\frac{-t}{2}} (\cos {\sqrt{7} \frac{t}{2}} + \frac{\sin {\sqrt{7} \frac{t}{2}}}{\sqrt{7}}) $$
verificabile online tramite Wolfram Alpha.
Le implementazioni dei risoluti qui di seguito richiedono che l'equazione differenziale del secondo ordine
sia scritta in forma esplicita come sistema di equazioni del primo ordine nel seguente modo:
$$ \begin{equation}
\begin{cases}
y=x'
\\
y'=F(x, y, t)
\end{cases}
\end{equation} $$
e quindi il problema di Cauchy iniziale si scrive equivalentemente nel seguente modo:
$$ \begin{equation}
\begin{cases}
y = x'
\\
y'= -y - 2x = 0
\\
x(0)=1
\\
y(0)=0
\end{cases}
\end{equation} $$
Scipy
Scipy utilizza la funzione scipy.integrate.solve_ivp
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali
che, per quanto detto prima, è equivalente all'equazione del secondo ordine con le stesse condizioni iniziali.
La forma esplicita del sistema di cui sopra in Python con NumPy si implementa così:
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return [dx_dt, d2x_dt2]Qui di seguito un esempio di codice Python che confronta la soluzione analitica del sistema con quella numerica ottenuta tramite
scipy.integrate.solve_ivp:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return [dx_dt, d2x_dt2]
an_sol_x = lambda t : \
np.exp(-t/2.) * (np.cos(np.sqrt(7) * t / 2.) + \
np.sin(np.sqrt(7) * t / 2.)/np.sqrt(7.))
t_begin=0.
t_end=12.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = 1.
dxdt_init = 0.
x_an_sol = an_sol_x(t_space)
method = 'RK45' #available methods: 'RK45', 'RK23', 'DOP853', 'Radau', 'BDF', 'LSODA'
num_sol = solve_ivp(ode_sys, [t_begin, t_end], [x_init, dxdt_init], method=method, dense_output=True)
X_num_sol = num_sol.sol(t_space)
x_num_sol = X_num_sol[0].T
plt.figure()
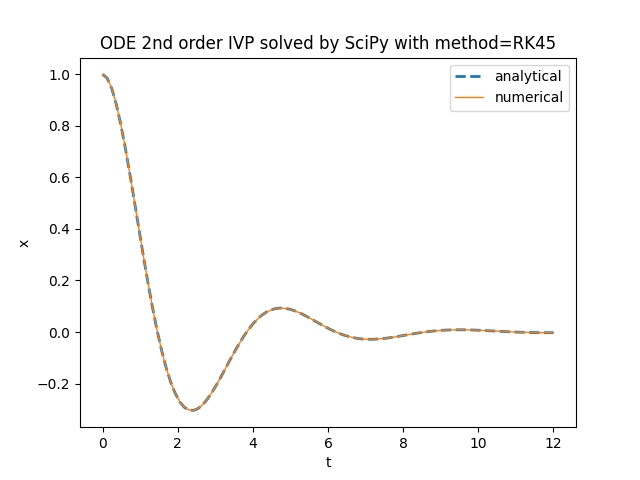
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 2nd order IVP solved by SciPy with method=' + method)
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
scipy.integrate.solve_ivp.TensorFlow Probability
TensorFlow Probability utilizza la classe tfp.math.ode.BDF
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valore iniziali
che, per quanto detto prima, è equivalente all'equazione del secondo ordine con le stesse condizioni iniziali.
La forma esplicita del sistema di cui sopra in Python con TensorFlow Probability si implementa così:
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return [dx_dt, d2x_dt2]Qui di seguito un esempio di codice Python che confronta la soluzione analitica del sistema con quella numerica ottenuta tramite
tfp.math.ode.BDF:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_probability as tfp
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return [dx_dt, d2x_dt2]
an_sol_x = lambda t : \
np.exp(-t/2.) * (np.cos(np.sqrt(7) * t / 2.) + \
np.sin(np.sqrt(7) * t / 2.)/np.sqrt(7.))
t_begin=0.
t_end=12.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
t_init = tf.constant(t_begin)
x_init = tf.constant(1.)
dxdt_init = tf.constant(0.)
x_an_sol = an_sol_x(t_space)
num_sol = tfp.math.ode.BDF().solve(ode_sys, t_init, [x_init, dxdt_init],
solution_times=tfp.math.ode.ChosenBySolver(tf.constant(t_end)) )
plt.figure()
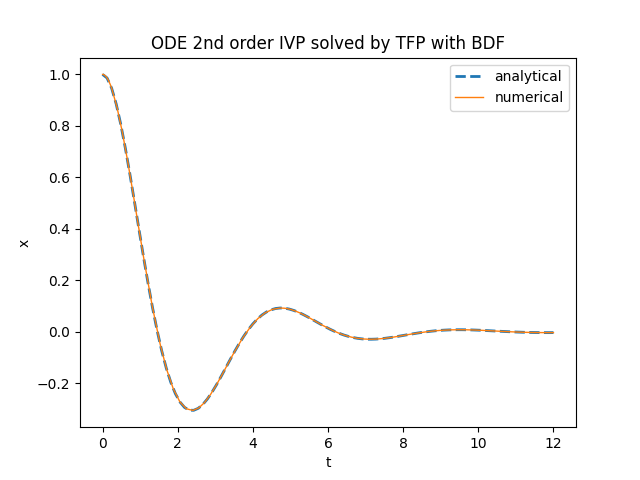
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(num_sol.times, num_sol.states[0], linewidth=1, label='numerical')
plt.title('ODE 2nd order IVP solved by TFP with BDF')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
tfp.math.ode.BDFTorchDiffEq
TorchDiffEq utilizza la funzione torchdiffeq.odeint
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali
che, per quanto detto prima, è equivalente all'equazione del secondo ordine con le stesse condizioni iniziali.
La forma esplicita del sistema di cui sopra di cui sopra in Python con Torch si implementa così:
def ode_sys(t, X):
x=torch.Tensor([X[0]])
dx_dt=torch.Tensor([X[1]])
d2x_dt2=torch.Tensor([-dx_dt - 2*x])
return torch.cat([dx_dt, d2x_dt2])Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
torchdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import torch
from torchdiffeq import odeint
def ode_sys(t, X):
x=torch.Tensor([X[0]])
dx_dt=torch.Tensor([X[1]])
d2x_dt2=torch.Tensor([-dx_dt - 2*x])
return torch.cat([dx_dt, d2x_dt2])
an_sol_x = lambda t : \
np.exp(-t/2.) * (np.cos(np.sqrt(7) * t / 2.) + \
np.sin(np.sqrt(7) * t / 2.)/np.sqrt(7.))
t_begin=0.
t_end=12.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = torch.Tensor([1.])
dxdt_init = torch.Tensor([0.])
x_an_sol = an_sol_x(t_space)
num_sol = odeint(ode_sys, torch.cat([x_init, dxdt_init]), torch.Tensor(t_space)).numpy()
plt.figure()
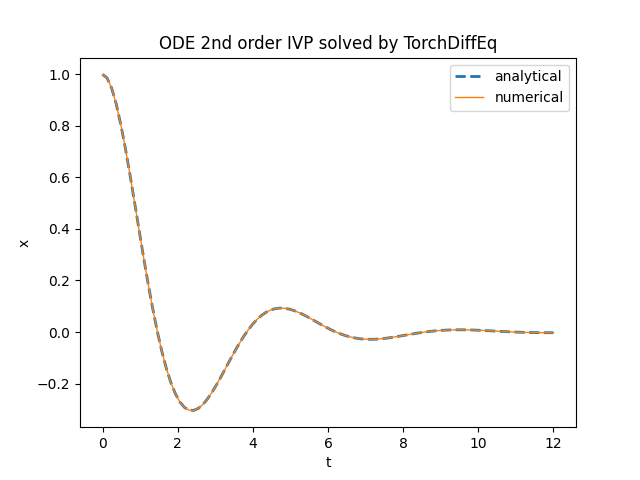
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, num_sol[:,0], linewidth=1, label='numerical')
plt.title('ODE 2nd order IVP solved by TorchDiffEq')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
torchdiffeq.odeint.TensorFlowDiffEq
TensorFlowDiffEq utilizza la funzione tfdiffeq.odeint
per risolvere numericamente un sistema di equazioni differenziali ordinarie del primo ordine con valori iniziali
che, per quanto detto prima, è equivalente all'equazione del secondo ordine con le stesse condizioni iniziali.
La forma esplicita del sistema di cui sopra in Python con Tensorflow si implementa così:
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return tf.stack([dx_dt, d2x_dt2])Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
tfdiffeq.odeint:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tfdiffeq import odeint
def ode_sys(t, X):
x=X[0]
dx_dt=X[1]
d2x_dt2=-dx_dt - 2*x
return tf.stack([dx_dt, d2x_dt2])
an_sol_x = lambda t : \
np.exp(-t/2.) * (np.cos(np.sqrt(7) * t / 2.) + \
np.sin(np.sqrt(7) * t / 2.)/np.sqrt(7.))
t_begin=0.
t_end=12.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = tf.constant([1.])
dxdt_init = tf.constant([0.])
x_an_sol = an_sol_x(t_space)
num_sol = odeint(
ode_sys,
tf.convert_to_tensor([x_init, dxdt_init], dtype=tf.float64),
tf.constant(t_space)).numpy()
plt.figure()
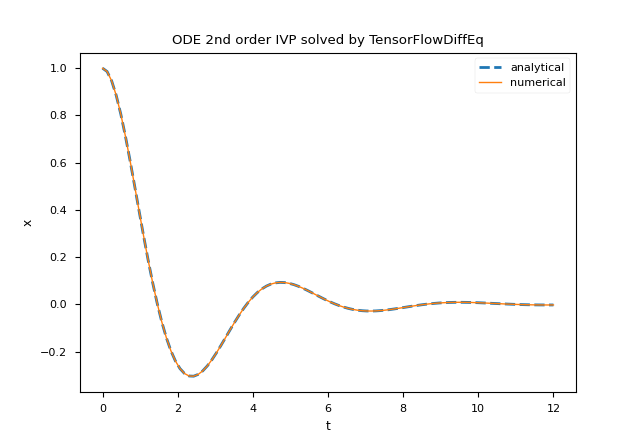
plt.plot(t_space, x_an_sol,'--', linewidth=2, label='analytical')
plt.plot(t_space, num_sol[:,0], linewidth=1, label='numerical')
plt.title('ODE 2nd order IVP solved by TensorFlowDiffEq')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
tfdiffeq.odeint.NeuroDiffEq
NeuroDiffEq è una libreria che utilizza una rete neurale implementata tramite PyTorch
per risolvere numericamente una equazione differenziale del secondo ordine con valori iniziali.
Il risolutore NeuroDiffEq presenta una serie di differenze rispetto ai precedenti risolutori.
Innanzitutto non è necessario riscrivere l'equazione del secondo ordine in un equivalente sistema di equazioni del primo ordine
poiché la libreria supporta nativamente le derivate di ordine superiore a uno,
infatti la funzione diff(x, t, order) consente di indicare la derivata prima passando order=1 e la derivata seconda passando order=2.
Per quanto detto sopra, questa libreria prende in input l'equazione in forma forma implicita, ovverosia:
$$ \begin{equation}
x'' + x' + 2x = 0
\end{equation} $$
e tenendo conto che la lambda (o la funzione) che rappresenta l'equazione ha la $t$ e la $x$ invertite di posizione rispetto a tutte le altre librerie viste prima,
la forma implicita dell'equazione di cui sopra in Python con Torch e NeuroDiffEq si implementa così:
ode_fn = lambda x, t: diff(x, t, order=2) + diff(x, t, order=1) + 2. * xLa libreria NeuroDiffEq utilizza la funzione
neurodiffeq.ode.solve per eseguire l'approssimazione della soluzione dell'equazione;
tale funzione prende in input (opzionalmente) una rete neurale, l'algoritmo di training e altri iperparametri.Qui di seguito un esempio di codice Python che confronta la soluzione analitica con quella numerica ottenuta tramite
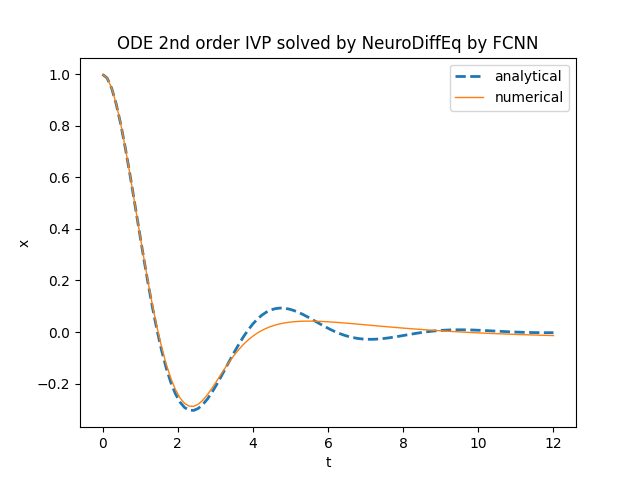
neurodiffeq.ode.solve
nell'intervallo $[0.0,12.0]$ con le seguenti impostazioni:
- rete neurale Fully Connected (abbreviata FC, detta anche MLP per multilayer perceptron) con 6 layer, 50 neuroni per layer e Tanh quale funzione di attivazione;
- algoritmo di ottimizzazione Adam con learing rate impostato a 0.002;
- batch size uguale a 200, numero massimo di epoche 500, flag best model impostato a True.
import numpy as np
import matplotlib.pyplot as plt
import torch
from neurodiffeq import diff
from neurodiffeq.ode import solve
from neurodiffeq.ode import IVP
from neurodiffeq.ode import Monitor
import neurodiffeq.networks as ndenw
ode_fn = lambda x, t: diff(x, t, order=2) + diff(x, t, order=1) + 2. * x
an_sol = lambda t : \
np.exp(-t/2.) * (np.cos(np.sqrt(7) * t / 2.) + \
np.sin(np.sqrt(7) * t / 2.)/np.sqrt(7.))
t_begin=0.
t_end=12.
t_nsamples=100
t_space = np.linspace(t_begin, t_end, t_nsamples)
x_init = IVP(t_0=t_begin, x_0=1.0, x_0_prime=0.0)
x_an_sol = an_sol(t_space)
net = ndenw.FCNN(n_hidden_layers=6, n_hidden_units=50, actv=torch.nn.Tanh)
optimizer = torch.optim.Adam(net.parameters(), lr=0.002)
num_sol, loss_sol = solve(ode_fn, x_init, t_min=t_begin, t_max=t_end,
batch_size=200,
max_epochs=500,
return_best=True,
net=net,
optimizer=optimizer,
monitor=Monitor(t_min=t_begin, t_max=t_end, check_every=10))
x_num_sol = num_sol(t_space, as_type='np')
plt.figure()
plt.plot(t_space, x_an_sol, '--', linewidth=2, label='analytical')
plt.plot(t_space, x_num_sol, linewidth=1, label='numerical')
plt.title('ODE 2nd order IVP solved by NeuroDiffEq by FCNN')
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.show()
neurodiffeq.ode.solve.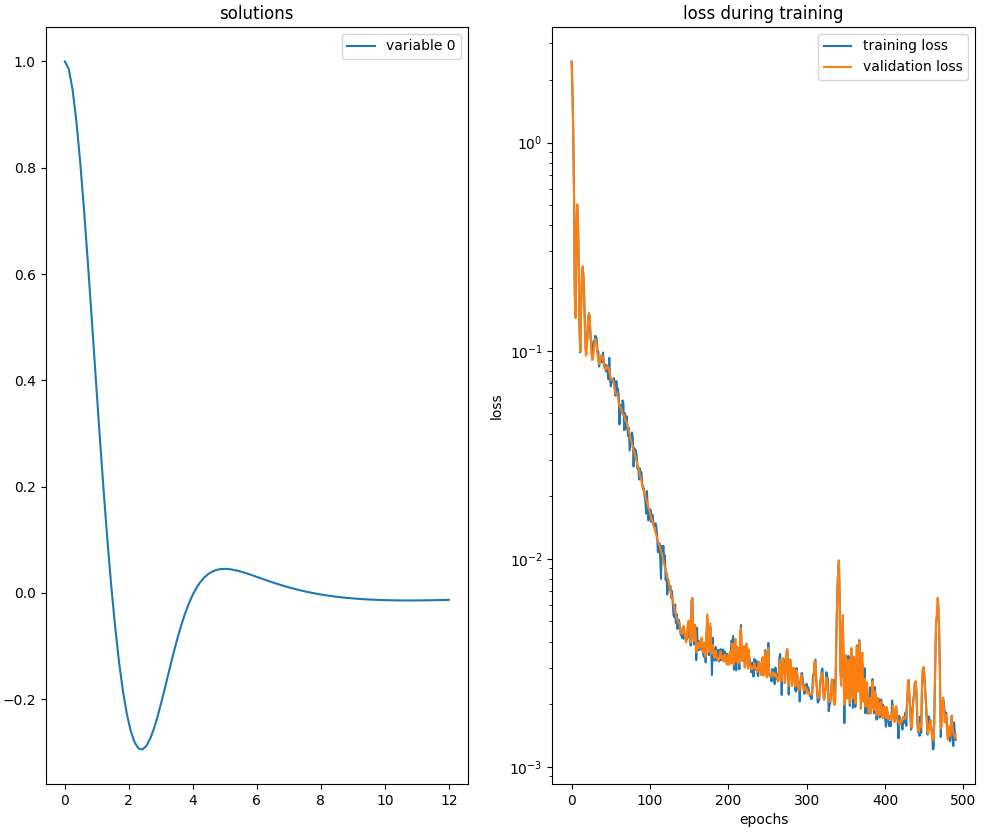
neurodiffeq.ode.solve.Download del codice completo
Il codice completo è disponibile su GitHub.
Questo materiale è distribuito su licenza MIT; sentiti libero di usare, condividere, "forkare" e adattare tale materiale come credi.
Sentiti anche libero di pubblicare pull-request e bug-report su questo repository di GitHub oppure di contattarmi sui miei canali social disponibili nell'angolo in alto a destra di questa pagina.