Random Numbers Generation
Generating random numbers on a quantum computer is not difficult because the unpredictability of measure of a qubit in a state of superposition it is in fact a form of natural randomness. Translating this idea into code is relatively simple: taking n qubits (therefore the random number obtained from each execution will be an integer from 0 to 2n - 1) with initial state equals to $|0\rangle$, the quantum Hadamard gate is applied to each of the n qubits and finally the measurement is performed. The quantum Hadamard gate applied to a qubit in $|0\rangle$ state brings it in superposition state: $$\frac{|0\rangle + |1\rangle}{\sqrt{2}}$$ and this means that the measure will have the probability of 50% to be equal to 0 and 50% to be equal to 1.
Circuit diagram
Considering that a quantum computer with 5 qubits is available, the circuit diagram that achieves the above is the following:
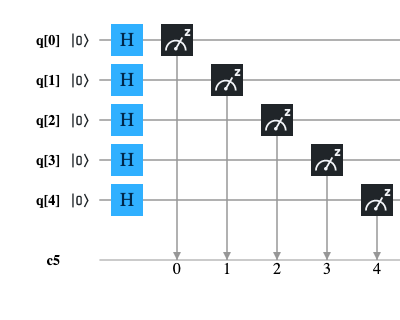
QASM code
The following program is the translation in QASM language of the circuit illustrated above; this program has been tested both on IBM's quantum computer 'ibmq_london' and on the IBM 'qasm_simulator' simulator.
OPENQASM 2.0;
include "qelib1.inc";
qreg q[5];
creg c[5];
h q[0];
h q[1];
h q[2];
h q[3];
h q[4];
measure q[0] -> c[0];
measure q[1] -> c[1];
measure q[2] -> c[2];
measure q[3] -> c[3];
measure q[4] -> c[4];Python with Qiskit code
The following program is the translation in Python with Qiskit of the circuit shown above; this program was tested inside a Jupyter Notebook using as backend both IBM's quantum computer 'ibmq_london' and IBM's 'qasm_simulator' simulator.
q = QuantumRegister(5, 'q')
c = ClassicalRegister(5, 'c')
circuit = QuantumCircuit(q, c)
circuit.h(q[0])
circuit.h(q[1])
circuit.h(q[2])
circuit.h(q[3])
circuit.h(q[4])
circuit.measure(q, c)Microsoft Q# .NET Core code for quantum simulator
The following program is the Microsoft Q# translation of the circuit shown above; this program has been tested on a Linux with .NET Core, Q# runtime and Microsoft quantum simulator installed.
namespace ComputationalMindset.QuantumExperiments
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Canon;
open Microsoft.Quantum.Measurement;
operation RandomNumberGenerator() : (Result, Result, Result, Result, Result)
{
using (q = Qubit[5])
{
H(q[0]);
H(q[1]);
H(q[2]);
H(q[3]);
H(q[4]);
let result = (M(q[0]), M(q[1]), M(q[2]), M(q[3]), M(q[4]));
ResetAll(q);
return result;
}
}
Results on IBM Q Experience
Both programs for IBM Q Experience were executed with a number of shots equals to 8192 both on the IBM's simulator 'qasm_simulator' and on the real computer IBM's 'ibmq_london' obtaining the expected result, ie a uniform distribution of all 5-bit combinations.
The imperfect uniformity shown in the case of real quantum computers compared to simulators is due to noise.
Note: Given the stochastic nature of this code, your specific reults may vary. Consider running the example a few times.

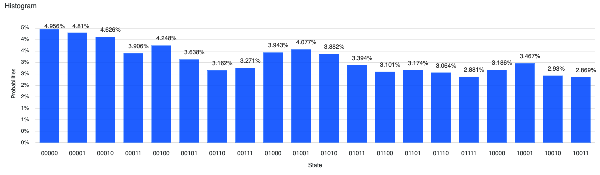
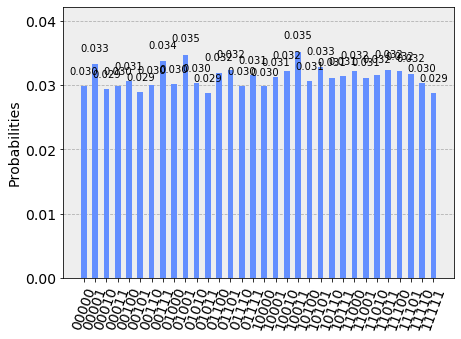
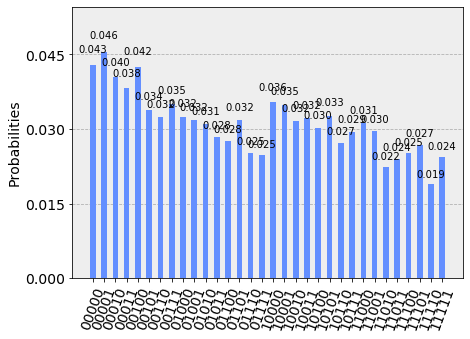
Results on Microsoft simulator
The execution of the Q# program for .NET Core produced the expected result, namely a uniform distribution of all 5 bits combinations.
Note: Given the stochastic nature of this code, your specific results may vary. Consider running the example a few times.
| Binary | Decimal | Count | Probability (%) |
|---|---|---|---|
| 00000 | 00 | 257 | 3.14% |
| 00001 | 01 | 265 | 3.24% |
| 00010 | 02 | 240 | 2.93% |
| 00011 | 03 | 255 | 3.11% |
| 00100 | 04 | 237 | 2.89% |
| 00101 | 05 | 265 | 3.24% |
| 00110 | 06 | 267 | 3.26% |
| 00111 | 07 | 255 | 3.11% |
| 01000 | 08 | 257 | 3.14% |
| 01001 | 09 | 256 | 3.13% |
| 01010 | 10 | 241 | 2.94% |
| 01011 | 11 | 246 | 3.00% |
| 01100 | 12 | 251 | 3.06% |
| 01101 | 13 | 264 | 3.22% |
| 01110 | 14 | 272 | 3.32% |
| 01111 | 15 | 265 | 3.24% |
| 10000 | 16 | 223 | 2.72% |
| 10001 | 17 | 244 | 2.98% |
| 10010 | 18 | 262 | 3.20% |
| 10011 | 19 | 245 | 2.99% |
| 10100 | 20 | 255 | 3.11% |
| 10101 | 21/td> | 248 | 3.03% |
| 10110 | 22 | 251 | 3.06% |
| 10111 | 23 | 256 | 3.13% |
| 11000 | 24 | 272 | 3.32% |
| 11001 | 25 | 267 | 3.26% |
| 11010 | 26 | 292 | 3.56% |
| 11011 | 27 | 227 | 2.77% |
| 11100 | 28 | 278 | 3.39% |
| 11101 | 29 | 262 | 3.20% |
| 11110 | 30 | 257 | 3.14% |
| 11111 | 31 | 260 | 3.17% |
| Totals: | 8192 | 100.00% | |
Media
Download of the complete code
The complete code is available at GitHub.
These materials are distributed under MIT license; feel free to use, share, fork and adapt these materials as you see fit.
Also please feel free to submit pull-requests and bug-reports to this GitHub repository or contact me on my social media channels available on the top right corner of this page.