Fitting functions with a configurable Support Vector Regressor

This post deals with the approximation of real mathematical scalar functions to one or more real variables using a PyCaret without writing code but only acting on the command line of Python scripts that implement the functionality of:

  • Regressor Configuration and training
  • Prediction and error calculation
The code described by this post requires Python version 3 and uses the SciKit-Learn library; it also requires the NumPy, Pandas, MatPlotLib and JobLib libraries.
To get the code please see the paragraph Download of the complete code at the end of this post.

For the generation of synthetic training and test datasets, the following common tools (available in the repository) will be used:
  • fx_gen.py for the real-valued scalar functions of one real-valued variable $f \colon [a,b] \to {\rm I\!R}$
  • fxy_gen.py for the real-valued scalar functions of two real-valued variables $f(x,y) \colon [a,b] \times [c,d] \to {\rm I\!R}$
  • pcm2t_gen.py for parametric curves on the plane, so real-valued vector functions $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R}$
  • pmc3t_gen.py for parametric curves in space, so real-valued vector functions $f(t) \colon [a,b] \to {\rm I\!R \times \rm I\!R \times \rm I\!R}$
Also for the visualization of the results, and precisely for the comparison of the test dataset with the prediction, the following common tools (always available in the repository) will be used:

Regressor Configuration and training

In this chapter two programs are presented: fit_func_esvr.py and fit_func_nusvr.py which technically are wrappers respectively of the classes sklearn.svm.SVR and sklearn.svm.NuSVR of the SciKit-Learn library and their purpose is to allow the use of the underlying regressors to fit functions without having to write code but only acting on the command line.
In fact through the argument --svrparams the user passes a series of hyper-parameters to adjust the behavior of the'underlying SVR algorithm and others to configure its learning phase. In addition to the parameters of the underlying regressor the program supports its own arguments to allow the user to pass the training dataset and on which file to save the trained model.

Both programs are of type M.I.M.O., that is Multiple Input Multiple Output: are designed to approximate a function of the shape $f \colon \rm I\!R^n \to \rm I\!R^m$ using in the implementation the sklearn.multioutput.MultiOutputRegressor class.
The format of the input datasets is in csv format (with header), with $n+m$ columns, of which the first $n$ columns contain the values of the $n$ independent variables and the last $m$ containing the values of the dependent variables.

Usage of the fit_func_esvr.py program

To get the program usage you can run this following command: 

$ python fit_func_esvr.py --help
and the output got is: 

usage: fit_func_esvr.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                        --outputdim NUM_OF_DEPENDENT_COLUMNS --modelout
                        MODEL_FILE [--dumpout DUMPOUT_PATH]
                        [--svrparams SVR_PARAMS]

fit_func_esvr.py fits a multiple-input multiple-output function dataset using
a configurable Epsilon-Support Vector Regressor

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --modelout MODEL_FILE
                        Output model file
  --svrparams SVR_PARAMS
                        Parameters of Epsilon-Support Vector Regressor
                        constructor
Where:
  • -h, --help: shows the usage of the program and ends the execution.

  • --version: shows the version of the program and ends the execution.

  • --trainds: path (relative or absolute) of a $n$+$m$ columns csv file (with header) that contains the dataset to be used for the training; this file can be generated synthetically e.g. via the program fx_gen.py. or be a dataset actually obtained by measuring a scalar and real phenomenon that depends on a single real-valued variable.

  • --outputdim: the $n$ number of independent variables that are the first $n$ columns of the csv dataset; the rest of the columns on the right are the $m$ dependent variables accordingly.

  • --modelout: path (relative or absolute) to a file where to save the trained model in joblib format (.jl).

  • --svrparams: list of parameters to pass to the regression algorithm below; see documentation of sklearn.svm.SVR.

Usage of the fit_func_nusvr.py program

To get the program usage you can run this following command: 

$ python fit_func_nusvr.py --help
and the output got is: 

usage: fit_func_nusvr.py [-h] [--version] --trainds TRAIN_DATASET_FILENAME
                         --outputdim NUM_OF_DEPENDENT_COLUMNS --modelout
                         MODEL_FILE [--dumpout DUMPOUT_PATH]
                         [--svrparams SVR_PARAMS]

fit_func_nusvr.py fits a multiple-input multiple-output function dataset using
a configurable Nu-Support Vector Regressor

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --trainds TRAIN_DATASET_FILENAME
                        Train dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --modelout MODEL_FILE
                        Output model file
  --svrparams SVR_PARAMS
                        Parameters of Nu-Support Vector Regressor constructor
Where:
  • -h, --help: shows the usage of the program and ends the execution.

  • --version: shows the version of the program and ends the execution.

  • --trainds: path (relative or absolute) of a $n$+$m$ columns csv file (with header) that contains the dataset to be used for the training; this file can be generated synthetically e.g. via the program fx_gen.py. or be a dataset actually obtained by measuring a scalar and real phenomenon that depends on a single real-valued variable.

  • --outputdim: the $n$ number of independent variables that are the first $n$ columns of the csv dataset; the rest of the columns on the right are the $m$ dependent variables accordingly.

  • --modelout: path (relative or absolute) to a file where to save the trained model in joblib format (.jl).

  • --svrparams: list of parameters to pass to the regression algorithm below; see documentation of sklearn.svm.NuSVR.

Prediction and error calculation

In this chapter the program predict_func.py is presented and which purpose is to make predictions on a test dataset applying it to a previously trained e-SVR or nu-SVR model respectively via the program fit_func_esvr.py or fit_func_nusvr.py, always without having to write code but only through the command line.
In fact, this program supports arguments through which the user passes the previously trained model, the test dataset and the error measurements to be calculated between the predictions and the true values.
The format of the incoming test datasets is identical to that of the training programs mentioned above; obviously here the last columns (those of dependent variables) are only used to compare the predicted values with the true values by calculating passed error measurements.

Usage of the predict_func.py program

To get the program usage you can run this following command: 

$ python predict_func.py --help
and the output got is: 

usage: predict_func.py [-h] [--version] --model MODEL_FILE --ds DF_PREDICTION
                       --outputdim NUM_OF_DEPENDENT_COLUMNS --predictionout
                       PREDICTION_DATA_FILE
                       [--measures MEASURES [MEASURES ...]]

predict_func.py makes prediction of the values of a multiple-input multiple-
output function with a pretrained Standard Vector Regressor model

optional arguments:
  -h, --help            show this help message and exit
  --version             show program's version number and exit
  --model MODEL_FILE    model file
  --ds DF_PREDICTION    dataset file (csv format)
  --outputdim NUM_OF_DEPENDENT_COLUMNS
                        Output dimension (alias the number of dependent
                        columns, that must be last columns)
  --predictionout PREDICTION_DATA_FILE
                        prediction data file (csv format)
  --measures MEASURES [MEASURES ...]
                        List of built-in sklearn regression metrics to compare
                        prediction with input dataset
Where:
  • -h, --help: shows the usage of the program and ends the execution.

  • --version: shows the version of the program and ends the execution.

  • --model: path (relative or absolute) to the file in joblib (.jl) format of the model generated by a training program mentioned above.

  • --ds: path (relative or absolute) of the csv file (with header) that contains the input dataset on which to calculate the prediction.

  • --outputdim: the $n$ number of independent variables that are the first $n$ columns of the csv dataset; the rest of the columns on the right are the $m$ dependent variables accordingly.

  • --predictionout: path (relative or absolute) of the csv file to generate that will contain the prediction, that is the approximation of the function applied to the input dataset.

  • --measures: list of measurements to be calculated by comparing the true values of the input dataset and the predicted output values; the list of supported metrics is defined in SciKit Learn Regression Metrics.

An example of using of all the programs

Suppose you want to approximate the function $$f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$$ in the range $[-10.0,10.0]$. Keeping in mind that np is the alias of NumPy library, the translation of this function in lambda body Python syntax is: 

0.5*x**3 - 2*x**2 - 3*x - 1
To generate the training dataset, run the following command: 

$ python fx_gen.py \
  --dsout mytrain.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.01
instead to generate the test dataset, run the following command: 

$ python fx_gen.py \
  --dsout mytest.csv \
  --funcx "0.5*x**3 - 2*x**2 - 3*x - 1" \
  --xbegin -10.0 \
  --xend 10.0 \
  --xstep 0.0475
Note that the discretization step of the test dataset is larger than that of training and it is a normal fact because the training, to be accurate, it must be run on more data. Also note that it is appropriate for the discretization step of the test dataset is not a multiple of the training one in order to ensure that the test dataset contains most of the data that is not present in training dataset, and this makes prediction more interesting.
To this we intend to make a regression by fit_func_esvr.py passing to the underlying regressor: kernel: rbf, C: 100, gamma: 0.1, epsilon: 0.1; then run the following command: 

$ python fit_func_esvr.py \
  --trainds mytrain.csv \
  --modelout mymodel.jl \
  --outputdim 1 \
  --svrparams "'kernel': 'rbf', 'C': 100, 'gamma': 0.1, 'epsilon': 0.1"
and at the end of the execution the saved mymodel.jl file contains the model of the e-svr regressor configured and trained.

Now we intend to perform the prediction and calculation of the error using the measurements mean_absolute_error and mean_squared_error; then execute the following command: 

$ python predict_func.py \
  --model mymodel.jl \
  --ds mytest.csv \
  --outputdim 1 \
  --predictionout mypred.csv \
  --measures mean_absolute_error mean_squared_error
and at the end of the execution the saved mypred.csv file contains the prediction performed by applying the model on the test data; the output of the program displays the error measures passed through the argument --measures and are acceptable: the first around $0.4$ and the second around $1.9$.
Note: Given the stochastic nature of the training phase, your specific results may vary. Consider running the training phase a few times.
Finally you want to make the comparative display of the test dataset with the prediction; therefore run the following command: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --title "e-svr ('kernel': 'rbf', 'C': 100, 'gamma': 0.1, 'epsilon': 0.1)" \
  --xlabel "x" \
  --ylabel "y=1/2 x^3 - 2x^2 - 3x - 1"
that shows the dispersion graphs of the test dataset and the superimposed prediction: in blue the one of the test dataset, in red the prediction. The comparison of the two graphs clearly shows that the approximation has reached very high levels.

Note: Given the stochastic nature of the training phase, your specific results may vary. Consider running the training phase a few times.

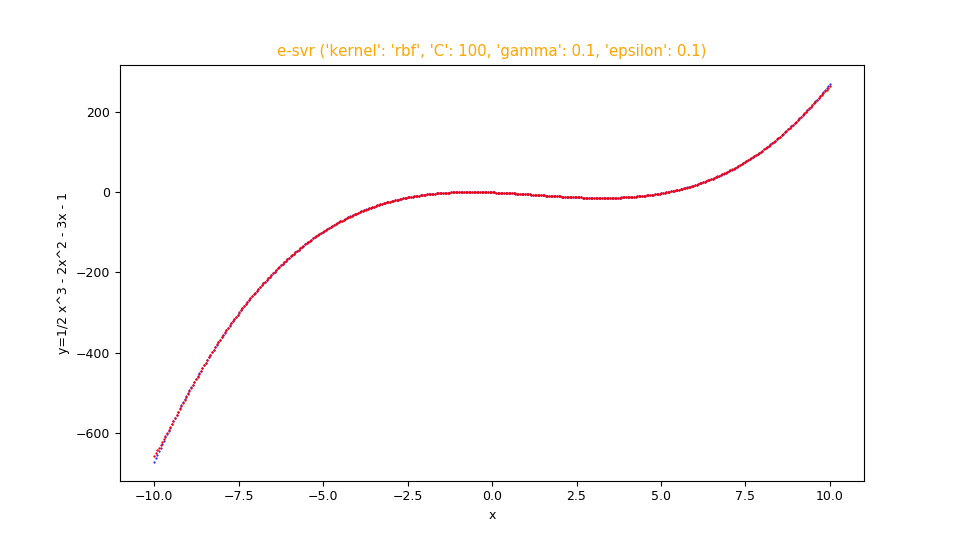
Figure with dispersion graphs generated by the program fx_scatter.py showing the fitting in red overlay of the function $f(x)=\frac {1}{2} x^3 - 2 x^2 - 3 x - 1$ and the original function below in blue.

If you want to make a regression by fit_func_nusvr.py switching to the underlying regressor: C: 10, gamma: auto then execute the following command: 

$ python fit_func_nusvr.py \
  --trainds mytrain.csv \
  --modelout mymodel.jl \
  --outputdim 1 \
  --svrparams "'C': 10, 'gamma': 'auto'"
then run the prediction using the predict_func.py command with the same parameters as above and finally to generate the dispersion graphs run the following command: 

$ python fx_scatter.py \
  --ds mytest.csv \
  --prediction mypred.csv \
  --title "nu-svr ('C': 10, 'gamma': 'auto')" \
  --xlabel "x" \
  --ylabel "y=1/2 x^3 - 2x^2 - 3x - 1"
The repository contains examples in shell scripts that show the use of these cascading programs:


Download of the complete code

The complete code is available at GitHub.
These materials are distributed under MIT license; feel free to use, share, fork and adapt these materials as you see fit.
Also please feel free to submit pull-requests and bug-reports to this GitHub repository or contact me on my social media channels available on the top right corner of this page.